Brückenschaltung gesamt Widerstand?
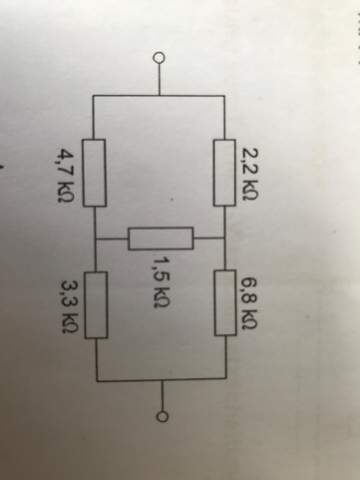
Ich möchte den gesamt Widerstand berechnen und irgendwie kriege ich es nicht gebacken.
2 Antworten
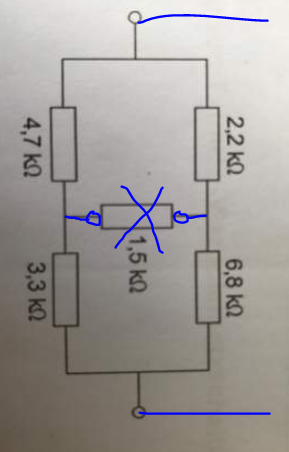
Man kann es so betrachten: Du hast ein "extra" Element, den 1,5kOhm Widerstand, der dich "stört".
Du kannst erst mal so tun, als ob dieser nicht da wäre (kein) - dann ist der Eingangswiderstand and den betrachteten Klemmen
R(kein) = (4k7+3k3)||(2k2+6k8) = 4,235k
Nun hast du aber ein zusätzliches Element Rx, welches man durch einen Korrekturfaktur c berücksichtigt. Dieser ergibt sich zu
c = (Rx+Rk)/(Rx+Ro)
Rk ist der Widerstand, den man an den Klemmen von Rx (ohne Rx) hineinmisst, wenn man die betrachteten Klemmen kurzschließt:
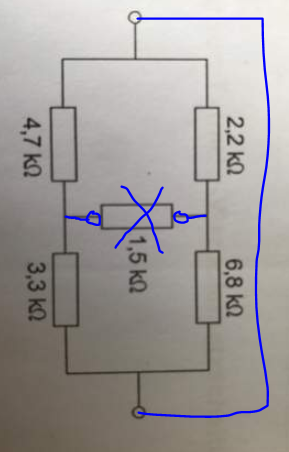
Das ergibt
Rk = (4k7||3k3) + (2k2||6k8) = 3,601k
Ro ist der Widerstand, den man an den Klemmen von Rx (ohne Rx) hineinmisst, wenn man die betrachteten Klemmen offen lässt:
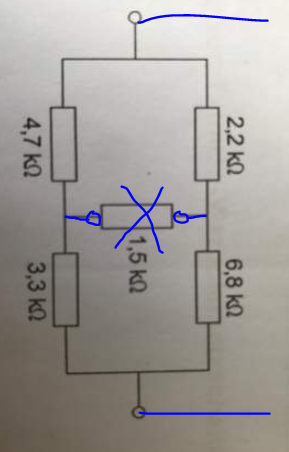
Das ergibt
Ro = (4k7+2k2) || (3k3+6k8) = 4,099k
Der Korrekturfaktor c wird somit
c = (1k5+3,601k)/(1k5+4,099k) = 0,911
Der gesuchte Eingangswiderstand ist also
R = R(kein)*c = 4,235k*0,911 ≈ 3,858 kOhm
Methode ist von Middlebrook - ich finde sie genial:
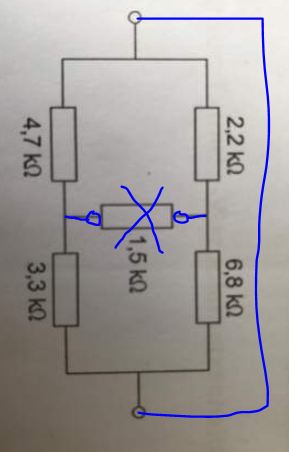
Stern-Dreieck Umwandlung muss natürlich genauso gehen...du hast da was falsch gemacht oder dich verrechnet.
genau komme jetzt auf den Wert 3,858268kOhm hatte bei Formel falsche Werte angegeben.
Hmmn, ich wers Morgen mal nachrrechnen. Meine Simulation auf die Schnelle ergibt 3.858kOhm.
Dürfte ich dich fragen mit welchen Simulator du es simuliert hast?
Ich danke für deine Hilfe.