Beispiel in Mikroökonomie Vollkommener Wettbewerb, Monopol, Presisdis 1. Grades
Ich kämpfe gerade mit folgendem Beispiel. Ich verstehe nämlich nicht wie ich nur aus der Nachfragekurve und den Durchschnitts=Grenzkosten den optimalen Output plus Preis errechnen kann. folgende Angabe geg: Nachfragekurve q=1400-50p und durchschnittskosten= grenzkosten= 8
ges: ist preis und output konsumentenrente produzentenrente im 1) vollkomennen wettbewerb 2) Monopol bzw Preisdiskriminierung 1. Grades
Wenn ich die Funktion integriere von 0-8 bekomme ich 9600 aber ob das meine rente ist weiß ich leider nicht. Ich hoffe es kann mir jemand einen gedankenanstoß geben lg
2 Antworten
Wenn die Durchschnittskosten in jedem Bereich den Grenzkosten entspricht, hat die Produktionsfunktion Konstante skalenerträge und die Kostenfunktion muss linear sein. K(q)=8q. Deine Nachfragefunktion löst du nach dem Preis auf. p=-1/50q+28. nun kannst du deine erlösfunktion aufstellen: E=p*q=(-1/50q+28)*q=-1/50q^2+28q. Nun gilt im Optimum : Grenzerlös=Grenzkosten. Also : -1/25q+28=8 => q=500. dann ist der Preis: -1/50*500+28=18GE. Beim Vollkommenen Wettbewerb ist G=0. das heißt:Preis=8 Einfach in deine Nachfragekurve einsetzen :1400-50*8=1000ME
Vielen Dank für die tolle Hilfe nun kann ich es rechnerisch einigermaßen nachvollziehen.
Ich habe nun so weit ich konnte den Grafen gezeichnet. (für Vollen Wettbewerb und Monopol)Nun ist mir aber nicht klar wie ich ohne Angebotskurve die Konsumentenrente bzw. Produzentenrente einzeichnen muss. Die Preisdiskriminierung 1. Grades bedeutet ja das jeder käufer die quasi den für sich höchsten preis zahlen würde z.b für einen preis von 24 würden 100 stück verkauft werden aber wie kann ich da die Rente berechnen bzw. einzeichnen?
LG
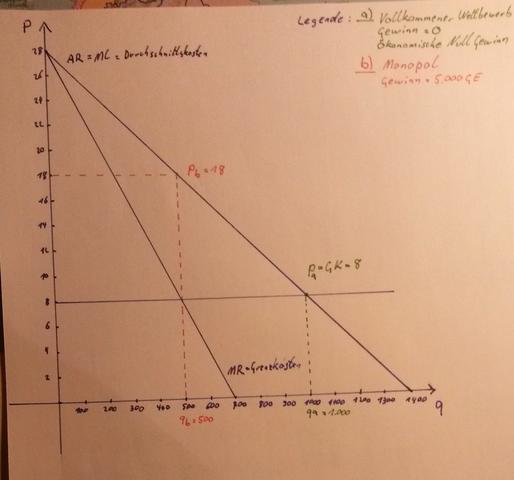
Bei der Preisdiskriminierung 1. Grades, verlangt der Monopolist von dem Nachfrager seine Zahlungsbereitschaft, daher den Höchstpreis den er zu zahlen bereit ist. Also ist die Konsumentenrente für jeden Nachfrager 0. denn Preis-Zahlenungsbereitschaft=Konsumentenrente. Daher erhält nur der Produzent eine Rente, die lautet :Produzentenrente = Preis-Kosten.