Bedinungen aus einem Graphen ablesen?!
Guten Abend, Wie meine Überschrift verrät geht es um Graphen, von denen man Punkte ablesen soll um Bedingungen aufzustellen für eine ganzrationale Funktion . Nur ich krieg es einfach nicht hin aus diesen Punkten Bedingungen zu machen.. vielleicht kann mir jemand helfen und es erklären. Danke Mfg
5 Antworten
Aufgabe a) geht sogar noch einfacher:
- Eine Nullstelle, die Berührpunkt ist, ist eine doppelte Nullstelle, und
- die dritte Nullstrelle ist ebenfalls gegeben.
- Vor dem Produkt der drei Linearfaktoren (mit der Form (x - x0), x0 ist je eine Nullstelle) steht noch der Leitkoeffizient a. Den kriegst du heraus, indem du die exakt ablesbaren Koordinaten des Maximums einsetzt.
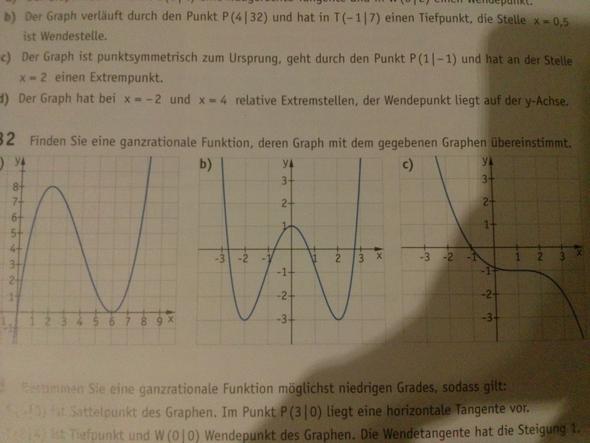
Zur Kontrolle: Ich bekomme y = -x²(x-6)/2
Aufgabe b) Ein Parameter lässt sich in der von KDWalther angegebenen Form
f(x) = ax^4 + bx² + c
direkt aus dem Graph ablesen.
- In f'(x) = 0 lässt sich x ausklammern;
- Einsetzen der Koordinaten eines geeigneten Extremums ergibt eine Bedingung für f, eine für f';
- das ergibt zwei Gleichungen mit je zwei Variablen.
Heraus kommt. y = x^4 /4 -2x² + 1
Aufgabe c) Der Graphs ergibt sich aus dem von y = -x³ durch
- Verschiebung in x- Richtung
- Streckung um einen einfachen Faktor in x-Richtung und
- Verschiebung in y-Richtung.
Diese drei Denkschritte ergeben in dieser Reihenfolge (!) ohne jede weitere Rechnung die Form des Terms, du brauchst dazu keine einzige Gleichung aufzulösen, kannst die Lösung direkt hinschreiben. (Vorsicht, Streckung und Verschiebung in x-Richtung verändern den Term "anders herum, als man denkt".)
Ausmultipliziert lautet der Term
y = -x³ /8+ 3x² /8 -3x/8 -7/8
@KDWalther. Wie du es machtest, finde ich auch absolut ok. Wäre deine Antwort nicht schon vorhanden gewesen, hätte ich auch einen solchen Weg vorgeschlagen.
Ansonsten bin ich dafür, das eine zu tun, und das andere nicht zu lassen. Die Pflicht und die Kür, sozusagen.
In der Praxis (von Aug zu Aug) halte ich das auch so. Ich lege sehr viel Wert darauf, mehrere Wege aufzuzeigen. Die Schüler sollen dann die Wege wählen, die ihnen persönlich am meisten zusagen - aus welchen Gründen auch immer.
Doch hier ist mir das manchmal einfach zu viel Tipparbeit :-)
Und bei c) wirst Du ausnutzen müssen, dass der Punkt (1|-1) ein Sattelpunkt (Wendepunkt mit waagerechter Tangente) ist.
Könnte man verwenden, aber es ist einfacher, wenn man Verschiebung und Streckung/Stauchung aus der Zeichnung abliest.
Stimmt. ich wolte bei meiner Hinführung zur Lösung diejenigen Kriterien benutzen, die bei jeder Funktion, egal welchen Typs, greifen. Zugegeben: in diesem Fall mit erheblich Mehrarbeit verbunden.
Die Frage im Bild ist etwas blöd formuliert. Besser ist:
Stellen sie die allgemeine Funktionsgleichung für folgende Grafen auf!
a) Funktion 3. Grades ohne Konstante, da durch P(0,0) gehend
b) Achssymmetrische Funktion 4. Grades, also ax^4 - bx² + 1
c) fallende Funktion 3. Grades ohne quadratisches Glied und aus P(0,0) nach rechts unten verschoben an einer fallenden Geraden (Linearglied):
-ax³ -bx - 0,8
folgende Grafen auf!
Graph(en). "Gra*f" ist ein Adelstitel. Aber das nur nebenbei:
c) fallende Funktion 3. Grades ohne quadratisches Glied und aus P(0,0) nach rechts unten verschoben an einer fallenden Geraden (Linearglied): -ax³ -bx - 0,8
Wie oft muss man dir eigentlich noch erklären, dass deine "Regeln" bzgl des linearen bzw quadratischen Gliedes völlig falsch sind? In diesem Fall hat der Funktionsterm zwar zufällig ein Linearglied, aber er hat durchaus auch ein quadratisches Glied.
Dies ist die Lösung für c):
f(x) = 1/8 * (x^3 - 3x^2 + 3x - 7)
Mit einem quadratischen Glied.
Wenn dies stimmen würdem, dann müsste man im Graph auch den Parabelansatz innerhalb von x³ sehen, ist jedoch nicht vorhanden!
Wenn dies stimmen würdem,
Es stimmt - außer, dass ich das "globale" Minus vergessen habe:
f(x) = -1/8 * (x^3 - 3x^2 + 3x - 7)
So ist es richtig. Und natürlich:
mit quadratischem Glieddann müsste man im Graph auch den Parabelansatz innerhalb von x³ sehen,
Nein, das müsste man nicht. Das ist nur eine fixe Idee von Dir.
Man hat dir dafür schon mehrfach Gegenbeispiele gegeben, die du jedesmal ignoriert hast.
Natürlich hat 1/8 * (x^3 - 3x^2 + 3x - 7) keinen "Parabelansatz" (der Herr Nachhilfelehrer war wieder zu bequem, die Funktion zu zeichnen und/oder eine Kurvendiskussion zu machen).
Muss ich das dem Herrn Nachhilfelehrer auch noch vorrechnen :-(
f(x) = -1/8 * (x^3 - 3x^2 + 3x - 7) | erste Ableitung
f´(x) = -1/8 * (3x^2 - 6x + 3)
Ableitung gleich Null setzen:
0 = -1/8 * (3x^2 - 6x + 3) | *(-8)
0 = 3x^2 - 6x + 3 | :3
0 = x^2 - 2x + 1 | zweite binomische Formel
0 = (x-1)^2
Die erste Ableitung hat eine doppelte Nullstelle bei x=-1. Man prüft leicht nach: das ist der Sattelpunkt, denn man auch in der Zeichnung erkennt.
Wenn man was auf die Schnelle korrigiert...
f(x) = -1/8 * (x^3 - 3x^2 + 3x + 7)
Ein "Plus" muss vor die 7. Ändert aber nichts an obiger Rechnung, das absolute Glied fällt beim Ableiten eh weg.
Funktion 3. Grades ohne quadratisches Glied und aus P(0,0) nach rechts unten verschoben an einer fallenden Geraden (Linearglied)
Und an anderer Stelle (hier (unten) aber auch früher, ich erinnere mich!) wurde von dir auch behauptet, dass, wenn ein quadratischen Glied vorhanden sei, dann gebe es Extremstellen ("Parabelansatz"). Ohne ein quadratischen Glied gebe es keine.
Dies ist falsch. Mal ohne den etwas aufgeregen Ton von schuhmode:
Die Funktion f(x)=x^3 nennen wir der Einfachheit halber hier "kubische Normalparabel", und von dieser gehen wir aus.
1. Lineares Glied, aber keine Verschiebungf(x) = x^3 + x
Ein lineares Glied, das einfach gleich x ist. Zeichnen! Man sieht, dass diese Funktion keineswegs durch Verschiebung entstanden ist, sondern durch Verformung der kubischen Normalparabel.
Eine Verformung ist ja auch viel eher zu erwarten; denn wenn man x oder 5x oder was immer zu einer Funktion addiert, dann wird ja an jeder Stelle was anderes addiert! Es ist eher erstaunlich, dass das manchmal tatsächlich zu einer Verschiebung des Graphen führt!
f(x) = x^3 - 3x^2 + 3x - 1
Wir haben ein quadratisches Glied, nämlich -3x^2, aber keine Extremstellen: Wenn man diese Funktion zeichnet, ergibt sich einfach der Graph der kubischen Normalparabel um 1 nach rechts verschoben.
3. Extremstellen, aber kein quadratisches Gliedf(x) = 1/3 * x^3 - x
Diese Funktion hat kein quadratisches Glied, aber zwei Extremstellen, nämlich
bei -1 und 1 (nachrechnen oder zeichnen!).
(Sie ist zugleich ein weiteres Beispiel einer Funktion mit linearem Glied, die aber nicht verschoben ist).
Von dem ursprünglichen Behauptungen ist praktisch nichts übriggeblieben!
Gezeichnet hab ich die Funktionen auch selbst, siehe: http://www.gutefrage.net/tipp/kein-zusammenhang-zwischen-linearem-glied-und-verschiebung-bzw-quadratischem-glied-und-extremstellen
Wie weit bist Du denn bislang gekommen?
Der Verlauf bei a) entspricht einer Funktion 3. Grades, also: f(x) = ax³ + bx² + cx + d. Dementsprechend brauchst Du vier Informationen/Bedingungen/Gleichungen.
Beispiel: Der Punkt (2|8) liegt auf dem Graphen, d.h. an der Stelle x = 2 nimmt die Funktion den Wert 8 an, kurz: f(2) = 8. Eingesetzt in Deinen Funktionsterm ergibt das die erste Gleichung: a·2³ + b·2² + c·2 + d = 8.
Auf diesem Weg suchst Du drei weitere Bedingungen; das können auch Infos über die Steigung... sein (z.B. f´(6) = 0).
Anschließend musst Du ein Gleichunsgsystem lösen.
Okey danke :-) Und bei b) hat man ja 3 extremstellen.. also ist das eine fu.ktion 4. Grades und man braucht 5 bedingungen oder ? Ich find aber nur 3 .. 2 Tiefpunkte und einen Hochpunkt
Okay.. ja die steigung ist dann 0 bei allen extremstellen. Aber dann hätte man ja 6 bedingungen oder ? Alle 3 extrempunkte + steigungen
Solange sich die Bedingungen nicht widersprechen (d.h. das Gleichungssystem lösbar ist), ist alles in Ordnung.
Aufgrund der Achsensymmetrie kannst Du aber mit f(x) = ax^4 + bx² + c rechnen und brauchst nur die positiven x-Wert zu betrachten. Dann hast Du wieder nur 3 (verwertbare) Gleichungen.
Hallo Elsenzahn!
Leider geht die Kommentar-Funktion nicht mehr.
Vielen Dank für deine 3 Beispiele. Ich habe mir 2 Tage den Kopf zerbrochen, um mein Wissen mit euren Lösungen in Übereinklang zu bringen. Ich habe über Verschiebung von höhergradigen Funktionen weder in LB's noch auf den Web-Matheseiten leider nichts gefunden ausser bei der quadratischen Funktion. Wahrscheinlich geht die reine Verschiebung nur bei dieser, weil bei allen anderen sich ja die äußere Form ändert. Ich habe auch keinen GTR, so daß ich die Werte im Kopf durchgerechnet habe. Ich muss erkennen, dass es Ausnahmen gibt, die meiner Regel widersprechen. Bei genauerem Hinsehen ist es bei den 3 Beispielen wahrscheinlich durch die Symmetrie der Einzelfunktionen (Glieder) so!
Danke für die Rückmeldung.
gefunden ausser bei der quadratischen Funktion.
Verschiebung durch addieren eines linearen Gliedes funktioniert in der Tat nur bei quadratischen Funktion.
Wahrscheinlich geht die reine Verschiebung nur bei dieser,
Verschieben kann man die schon, das muss man dann aber anders machen.
Ich habe über Verschiebung von höhergradigen Funktionen weder in LB's noch auf den Web-Matheseiten leider nichts gefunden ausser bei der quadratischen Funktion.
y = f(x)
dann ist f(x-1) um 1 nach rechts verschoben, egal was für ein Funktion das f ist.
- sin(x-1) : Sinus-Funktion um 1 nach rechts verschoben.
- e^(x-1) : e-Funktion um 1 nach rechts verschoben.
- (x-1)^3 : kubische Parabel um 1 nach rechts verschoben.
So einfach. Das haben wir schon in der Mittelschule irgendwann mal gemacht.
Wahrscheinlich geht die reine Verschiebung nur bei dieser,
*Augenroll* - das sagt einem doch schon die Anschauung, dass eine Verschiebeung immer möglich sein muss!.
weil bei allen anderen sich ja die äußere Form ändert.
Das kommt die bloß so vor, weil du die fixe Idee hast, alles über Addition irgendwelcher Glieder machen zu wollen. Das funktioniert i.d.R. aber nicht (warum sollte es auch?).
Ich muss erkennen, dass es Ausnahmen gibt, die meiner Regel widersprechen. Bei genauerem Hinsehen ist es bei den 3 Beispielen wahrscheinlich durch die Symmetrie der Einzelfunktionen
Bei genauerem Hinsehen hätte dir folgendes auffallen müssen: Beginne ich mit einer kubischen Parabel in der "Grundform" y=x^3, oder meinetwegen auch y=ax^3 und addiere dann eine lineares Glied bx, dann erhalte ich: ax^3+bx. Hier kommen aber nur ungerade Exponenten vor, die Funktion ax^3+bx ist also noch immer punktsymmetrisch zum Ursprung, genau wie die Ausgangsfunktion ax^3.
Also kann die Funktion garnicht veschoben worden sein! Folglich gibt's bei kubischen Parabeln der Form y=ax^3 KEINEN EINZIGEN FALL wo ein linearers Glied zu einer Verschiebung führen würde!
Von wegen "Ausnahmen"!
Folglich gibt's bei kubischen Parabeln der Form y=ax^3 KEINEN EINZIGEN FALL wo ein linearers Glied zu einer Verschiebung führen würde!
PS: Man kann sich leicht überlegen, dass das sogar für alle differenzierbaren Funktionen in KEINEN EINZIGEN FALL richtig ist, außer für die quadratischen.
Ich gebe gerne zu: es hätte einfachere Wege gegeben als die von mir vorgeschlagenen. Doch ich wollte auf einen Weg hinführen, der wirklich immer klappt und habe mich dabei an der Fragestellung von Simso orientiert.
Zudem ist die Frage, ob so etwas wie doppelte/dreifache Nullstelle oder Linearfaktorzerlegung im Unterricht dran war. Das wird längst nicht immer behandelt. So werden den Schülern häufiger die einfacheren Wege "versperrt" und sind dann evtl. auch als Lösungsweg nicht akzeptiert - leider!