Abschnittsweise definierte Funktionen. Flächeninhalt berechnen?
Hallo,gegeben sind die abschnittweise definierte Funktionen
f (a,b) (x) = {(1/5)x^3+x^2-(4/5)x-4 für x [kleiner gleich] -1 und {ax^2 + bx} für x > -1
Hab die Funktion als Foto im Anhang. Ist übersichtlicher
Nun ist gegeben, dass a=23/5 und b=7 ist."Die Funktion heißt nun f und ihr Graph Gf.
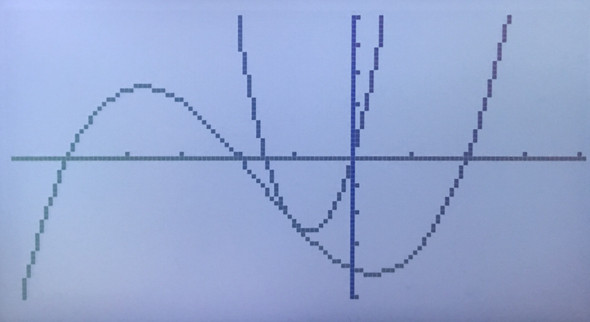
Der Graph Gf und die x-Achse schließen 2 Flächen vollständig ein. Ich soll den Inhalt der Gesamtfläche berechnen.
Mein Problem ist, dass ich keinen Ansatz finde, wie ich den Flächeninhalt von einer abschnittsweise definierten Funktion berechnen soll.
Ist mit Gf die komplette abschnittsweise definierte Funktion gemeint?
Habt ihr vielleicht einen Ansatz für mich, mit welcher Funktion ich jetzt rechnen muss?Wie ich mit einer "normalen" Funktion den Flächeninhalt ausrechnen muss, weiß ich.
Dankeschön!
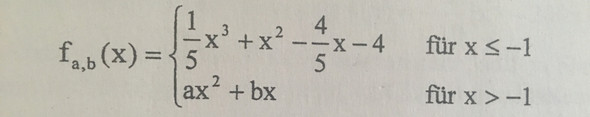
1 Antwort
Sei f₁(x) = 0,2x³ + x² - 0,8x - 4 und f₂(x) = 4,6x² + 7x
und F₁(x) und F₂(x) die jeweilige Stammfunktion. Dann ist die gesuchte Fläche
F₁(- 2) - F₁(- 5) + | F₁(- 1) - F₁(- 2) | + | F₂(0) - F₂(- 1) |