Ja, haben sie, denn was sind Hertzsche Wellen? Es sind spezielle elektromagnetische Wellen, benannt nach dem Physiker H. Hertz, der 1888 erstmals die Existenz elektromagnetischer Wellen nachwies.
Beste Grüße,
C. F. Gauß - princeps mathematicorum.
Ja, aber in dem Fall empfehle ich dir, dich mal hier einzulesen: https://physikunterricht-online.de/jahrgang-12/radioaktiver-zerfall/
0,7 kg sind 70% von 1 kg, also rechnest du:
Beste Grüße,
C. F. Gauß - princeps mathematicorum.
Ich habe falsch gelesen. Nacheinander also... beginnen wir mit F1. Wenn F1 wirkt, bewegt sich der Schwamm nach rechts. Wirkt danach F2, dann bewegt sich der Schwamm nicht mehr, weil F1 und F2 vom Betrag her gleichgroß sind, aber in entgegengesetzter Richtung (Kräfte sind ja vektorielle Größen). Wirkt jetzt F3, dann wird der Schwamm nach oben gedrückt (verschiebt sich aber weder nach rechts noch nach links, dafür sorgen ja F1 und F2). Wirkt anschließend F4, dann verharrt der Schwamm in Ruhe, da sich nun alle Kräfte ausgleichen (F3 ist vom Betrag her genauso groß wie F4 nur auch wieder entgegengesetzt).
Soll ich jetzt die 4 Kräfte die ich jetzt kenne zu einer der F's zuordnen und auch die Wirkung dazu schreiben? Oder rede ich da totalen Humbuck?
Was genau meinst du mit F's ? Also alle Kräfte sind betragsmäßig gleich groß und entgegengesetzt, womit sich in Summe keine Kraft ergibt und damit der Schwamm ruht, was auch nicht sonderlich verwunderlich ist. Aber du sollst einfach nur diese 4 Kräfte benennen, deren Wirkung angeben und sonst nichts weiter. Auch nicht zusammenfassen oder interpretieren.
Nein, dein Ergebnis stimmt nicht, obwohl dein Ansatz ein richtiger war, es gilt schon:
weil die Bewegung hier mit gleichförmig ist, allerdings ist deine Äquivalenzumformung misslungen, setzt man jetzt die Werte ein, ergibt sich eine Zeit von ungefähr 8 Minuten.
Beste Grüße,
C. F. Gauß - princeps mathematicorum.
Damit die zweidimensionalen Vektoren gleich sind, muss folgendes LGS erfüllt sein:
Löst man die obere Gleichung nach x auf, ergibt sich:
Fügen wir dies für unser x in die zweite Gleichung ein:
Jetzt ermitteln wir noch unser x, z.B. mit der ersten Gleichung:
Damit lauten die Lösungen für x und y:
Beste Grüße,
C. F. Gauß - princeps mathematicorum.
Nicht nur theoretisch, sondern auch praktisch.
Es kann also legitim geschrieben werden:
aber genauso gut kann auch ein Komma im Nenner vorkommen oder sowohl als auch.
Beste Grüße,
C. F. Gauß - princeps mathematicorum.
Nein und das ist auch gut so. Mathematik ist praktisch angewandte Logik.
Also erstmal würde ich hier das Einsetzungsverfahren präferieren, da diese Gleichung für mich schon förmlich danach schreit:
und dann für y in die andere Gleichung einsetzen...
Aber wenn du unbedingt das Additions-/bzw. Subtraktionsverfahren verwenden möchtest, dann kannst du z.B. wie du schon vorgeschlagen hast die zweite Gleichung durch -4 dividieren und die beiden zusammenaddieren.
-3x + 3x = 0, die x-Terme fallen also weg.
-y + y = 0 und auch die y-Terme fallen weg.
Es bleibt also 0 = 0 und damit hat das LGS unendlich viele Lösungen.
Beste Grüße,
C. F. Gauß - princeps mathematicorum.
NACHTRAG: Ich korrigiere meine erste Aussage dahingehend, dass man schon an den beiden Gleichungen sieht, dass die zweite Gleichung ein Vielfaches der ersten ist und somit schon klar sein sollte, dass unendlich viele Lösungen folgen ^^
Bedeutet graphisch dann, dass die beiden Geraden identisch sind:
Du kennst die Formel und kannst die Aufgabe trotzdem nicht lösen? Das finde ich sehr suspekt, denn es gilt für das Volumen einer Kugel:
Pi ist eine irrationale Konstante und das einzige, was hier variabel ist, ist der Radius r und der ist ja eindeutig gegeben. Rechnet man mit SI-Einheiten, also hier Meter anstelle Kilometer, ergibt sich nach der von mir genannten Formel:
Beste Grüße,
C. F. Gauß - princeps mathematicorum.
Zefix! Da moust do ned 4:67 rechnen, wenn douh steht 6792:4 ^^
Okay, ernsthaft...
Du schaust zunächst, wie oft die 4 in die 6 passt, rechnest also zunächst 6:4, dann notierst du dir rechts hinterm Gleichheitszeichen eine 1 und schreibst unten was 1*4 ist, also 4 und das subtrahierst du von der oberen Zahl, also hier 6:
6-4=2
Jetzt geht es weiter mit 2:4, da bekommst aber keine Zahl größer oder gleich 1 heraus, weshalb du die nächste Zahl herunterholst (hier eine 7). Also dividierst du letztlich 27:4 und da passt die 4 sozusagen 6 mal (ganzzahlig betrachtet) rein. Und jetzt wieder die 6 hinterm Gleichheitsszeichen notieren (haben bis jetzt 16 dort steht) und 6*4 unten und vom oberen subtrahieren:
27-24=3
So jetzt 3:4, geht auch schlecht, also die 9 herunterholen, macht also 39:4 und das geht ganzzahlig gesehen 9 mal. Schreibst also wieder rechts nach dem Gleichheitszeichen diese 9 hinter der 16 -> 169 und dann wieder 9*6 und das obere von dem Produkt abziehen:
39-36=3
Und auch hier wieder eine Zahl herunterholen, hier die 2 und das übliche Prozedere: Also rechts eine 8 dazu notieren dann 32-8*4, also 32-32 = 0, also kein Rest und damit bleibt stehen: 6792:4=1698
Was genau ist die Aufgabe? Also was sollst du mit diesem komplexen Polynom tun? Ich vermute mal Nullstellen bestimmen...
Es gibt genau eine reelle Lösung und drei komplexe.
Für die reelle Lösung:
Du bildest also ein Produkt und wendest dann den Satz vom Nullprodukt an:
womit wir unsere reelle Lösung hätten.
Für die komplexen Lösungen betrachtet man die andere Klammer:
und kommst dann zu den komplexen Lösungen:
Beste Grüße,
C. F. Gauß - princeps mathematicorum.
Verstehe ich nicht. Du brauchst Hilfe bei der Berechnung, willst aber auch wissen, was am Ende herauskommt. Also was denn jetzt? Willst du einen Rechenweg oder die Lösung? Die Determinante der Koeffizientenmatrix ist übrigens ungleich Null (genauer gleich Drei). Du könntest also nach der Cramerschen Regel das LGS lösen.
Das hast du richtig erkannt und ist tatsächlich de facto einfach nur schlecht bzw. falsch ausgedrückt. In der Regel meinen z.B. COD-Spieler damit, dass sie nach einem Game eine Kill-/Death-Quote (kurz: K/D) von < 1 haben. Das Schlechteste, was man erzielen kann, ist eine K/D von Null und das erreicht man eben bei Null Kills.
Beste Grüße,
C. F. Gauß - princeps mathematicorum.
Wenn es schon logische Probleme mit Gott gibt, ist dieser dumme Hokospokus doch komplett redundant. Verlass dich lieber auf deinen gesunden Menschenverstand, anstelle auf ein dämliches Spukbrett.
Wieso verstehst du sie nicht? Das würde mich mal interessieren. Ich meine, was ist so unklar, dass du nicht einmal eine Teilaufgabe bewerkstelligen kannst? Die Funktion f ist eindeutig auf ℝ definiert.
Ein sechsseitiges Prisma besitzt ein regelmäßiges Sechseck als Grundfläche G. Alle sechs Seitenflächen sind rechteckig, es gilt:
Grundsätzlich finden in jedem Wechselstromkreis elektromagnetische Schwingungen statt, weshalb sie als empirischer Nachweis herangezogen werden können (s. Schwingkreis https://www.abiweb.de/physik-elektromagnetismus/elektromagnetische-schwingungen/elektromagnetischer-schwingkreis.html).
Indirekt aber auch durch elektromagnetische Wellen, deren Existenz durch den Physiker J. C. Maxwell bereits 1868 vorausgesagt wurden. Denn Wellen sind bekanntermaßen sich räumlich ausbreitende Schwingungen, die Energie transportieren. Strahlung von Handy, Mikrowelle oder anderen technischen Geräten sind elektromagnetische Wellen in bestimmten Frequenz- bzw. Wellenlängenbereichen.
Der Satz des Pythagoras ist ein Spezialfall vom Cosinussatz, für den gilt:
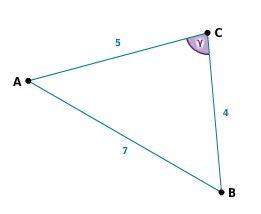
Ist das Dreieck rechtwinklig, z.B. hier unser 𝛾 = 90° groß, dann entfällt der Term:
und es bleibt letztlich die bekannte Formel stehen:
die wir als Satz des Pythagoras bezeichnen, freilich den antiken Ägyptern schon bekannt war und damit kein Verdienst von Pythagoras von Samos, wie der Name zunächst offenbaren mag.
Bedeutet also, ist das Dreieck rechtwinklig, wendest du den Satz des Pythagoras an, ist es das nicht, konstruierst du ein rechtwinkliges Dreieck, z.B. durch durch das Anlegen einer Orthogonalen (Senkrechte) oder benutzt doch den Cosinussatz.
Ich weiß jetzt nicht genau, was du mit:
Und woe gehen nochmal gleichungen😂
meinst, aber es reicht, wenn du ihn und die Vorgehensweise verinnerlichst bzw. verstehst.
Beste Grüße,
C. F. Gauß - princeps mathematicorum.