Wie löst man Reibungsaufgaben zeichnerisch?
Hallo zusammen :)
Sitz' gerade an 'ner alten Prüfungsaufgabe für's Studium und komme nicht weiter. Vielleicht findet sich hier jemand, der mir weiterhelfen kann.
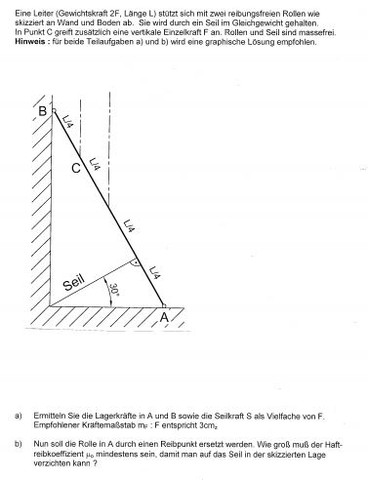
Die Aufgabe befindet sich im Anhang. Mit Aufgabenteil a.) gibt's keine Probleme. Wurde nach dem Culmann-Verfahren grafisch gelöst.
Aufgabenteil b.) bekomme ich aber weder zeichnerisch, noch rechnerisch hin.
Habe bislang versucht durch R = N * mü mit R = Fs (Seilkraft) auf die Lösung zu kommen. Hat nichts funktioniert. Genau das selbe gilt für die x-Komponente von Fs mit Fsx = cos 30° x Fs zu berechnen. Auch nicht richtig.
Leider komme ich nicht weiter und würde mich über Rechnungen oder Tipps freuen!
Die Musterlösung meines Profs ist : mü > 0,3368.
Vielen Dank im Voraus für jede Hilfe ;)
1 Antwort
Rechnerisch würde ich hinbekommen, aber wie man das zeichnerisch löst weiß ich nicht :D aber villeicht hilft dir der Rechenweg ja weiter.
Ich würde die Leiter erstmal freischneiden. Dann hat man in vertikaler Richtung die Kräfte F_G, F_C und die Lagerkraft F_A und in horizontaler Richtung die Lagerkraft F_B und unten die Reibkraft F_A*mü.
F_G und F_C sind ja gegeben, das heißt wir haben noch 3 Unbekannte (mü, F_A, F_B) für die wir noch 3 Gleichungen brauchen. Da würde ich das Gleichgewicht in horizontaler Richtung
F_B - F_A*mü = 0 (1)
in vertikaler Richtung
F_A - F_G - F_C = 0 (2)
und dazu noch das Momentengleichgewicht um A nehmen
F_G*L/2*cos(60)+F_C*3L/4*cos(60)-F_B*L*cos(30) = 0 (3)
Dann (3) nach F_B umformen und F_G = 2F und F_C = F einsetzen :
F_B = (F*cos(60)+0,75F*cos(60))/cos(30)
aus (2) kriegt man F_A= 3F
und dann alles in (1) einsetzen:
mü = F_B/F_A = (1,75*cos(60)/cos(30))/3
Ich hoffe das war verständlich und hilft dir weiter :)