Wie löse ich die Textaufgabe (Differentialgleichung)?
Hallo, ich komme bei einem mathematischen Problem nicht weiter. Ich wäre froh, wenn mir jemand helfen könnte. So frei wie möglich beschrieben lautet die Aufgabe wie folgt:
Zwei Autos fahren aufeinander zu. Das eine Auto bremst so ab, dass seine Geschwindigkeit proportional zum Abstand ist, während das andere Auto mit konstanter Geschwindigkeit weiterfährt. Wann kommt es zu einem Unfall?
Gegeben seien die anfänglichen Geschwindigkeiten und der anfängliche Abstand. Viele Dank im Voraus!
3 Antworten
So eine Aufgabe habe ich noch nie gerechnet.
1) zeichne zuerst mal ein x-y-Koordinatensystem
2) zeichne den Vektor V1=konstant ein,Anfang ligt im Ursprung
3) zeichne S0 ein,denn Abstand der Autos zum Zeitpunkt t=0 , liegt rechts vom Ursprung
4) zeichne den Vektor V2 ein,Anfang liegt bei So rechts und zeigt nach den Ursprung
Nun wählst du V1=20 m/s und V2=30m/s und So=1000 m
Nun wählst du eine Schrittweite von t=1 s
S1=v1*t
S2=V2*t
Abstand Ab=S0-(S1+S2)
V2=-m*Ab wählen wir m=-2m/s
Die Werte trägst du in eine Wertetabelle ein und zeichnest dann die Kuve auf
Ab(t)=...
So hast du wenigstens den angenäherten Kurvenverlauf und kannst dann deine rechnung überprüfen,ob sie überhaupt stimmt.
Tipp: Noch besser ist es,wenn du das in einen GTR programmierst,dann kannst du eine Schrittweite von t=0,1s nehmen oder noch kleiner,dann ist die Rechnung genauer.
ja, numerisch geht’s schon. Wollte es aber analytisch :-) Antwort inzwischen weiter unten! Trotzdem danke
Zu Beginn (t=0) hast Du ja folgende Situation:

Das rote Auto (Position s2(t)) faehrt mit konstanter Geschwindigkeit v (nach links), das gruene Auto (Position s1(t)) sei das, das abbremst. Wir wissen zunaechst:
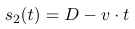
Die Geschwindigkeit des gruenen Autos ist proportional zum Abstand zum roten Auto, also:
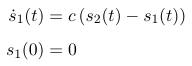
Die Proportionalitaetskonstante c liesse sich natuerlich auch durch die Startgeschwindigkeit des gruenen Autos ausdruecken. Dies ist eine inhomogene gewoehnliche Differentialgleichung erster Ordnung fuer die Position s1. Durch die Startbedingung ist die Loesung eindeutig festgelegt und laesst sich z.B. mittels Variation der Konstanten bestimmen (vgl. https://de.wikipedia.org/wiki/Variation_der_Konstanten#Lineare_Differentialgleichung_erster_Ordnung). Die Loesung lautet:
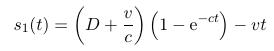
Daraus laesst sich nun natuerlich auch der Zeitpunkt tC des Zusammenpralls bestimmen; man erhaelt:
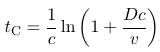
Ein typischer Zusammenstoss im Weg-Zeit-Diagramm saehe so aus:
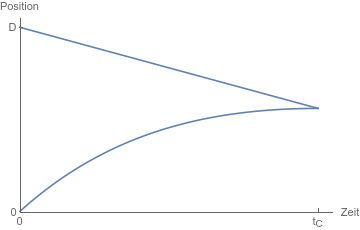






Hier findet sich auch eine allgemeine Loesungsformel fuer derartige Differentialgleichungen:
https://www.gutefrage.net/frage/dgl-einer-rakete-mit-veraenderlicher-masse-loesen#answer-268270132
Ich hatte so eine Aufgabe auch noch nie gerechnet. Die Bedingung, dass ein Fahrer genau so abbremst, dass das Verhaeltnis aus eigener Geschwindigkeit zum Abstand konstant bleibt, scheint mir auch sehr kuenstlich.
Die Frage traegt ja schon den Tag "Differentialgleichung"; daher gehe ich davon aus, dass es sich einfach um eine Uebungsaufgabe zur Variation der Konstanten handelt. In Schulbuechern wuerde ich die Aufgabe nicht erwarten, aber in Uni-Uebungsbuechern zur klassischen Mechanik koenntest Du vielleicht fuendig werden.
Die Fragestellung habe ich damals selbst konstruiert um ein analoges Problem in meinem Projekt in der Uni zu lösen. Ich wusste, dass es etwas mit Differentialrechnung zutun hat, aber ich konnte mich nicht mehr erinnern, wie das nochmal ging. Sorry für die verspätete Antwort :-)
Ich mach das hier nur aus Hobby und weil ich nicht einrosten will.
Ich habe Maschinenbau an einer Fachhochschule studiert.
ich mach das hier auch aus Mitleid,weil die Schüler kaum eine vernünftige Unterstützung haben.
Bis zu 80%,was die Schüler lernen,wird später eh nie mehr gebraucht.
Motto im System:"Just for fun and nice to have !"
Es ist a = - k • s mit einer Konstanten k.
Diese Differentialgleichung hat die allgemeine Lösung
s = c1 • sin(√k • t) + c2 • cos(√k • t)
Nun ist s(0) der Anfangsabstand der beiden Autos, v(0) ist die Summe der beiden Anfangsgeschwindigkeiten der Autos.
Nun s(t) zweimal ableiten, jeweils die Anfangsbedingungen einsetzen und damit c1 und c2 .
Ich sehe gerade, dass ich mich verlesen habe. Die Geschwindigkeit soll proportional zum Abstand sein, ich habe aus Versehen gelesen, dass die Beschleunigung proportional zum Abstand ist. Damit ist meine Lösung falsch (bezogen auf die Aufgabenstellung), die von BatesFan ist richtig (er kann offensichtlich besser lesen als ich :-))
Echt schöner Beitrag!! Werde ich noch nachrechnen und in meiner Aufgabensammlung aufnehmen.
Solch eine Aufgabe habe ich noch nie gerechnet.
Kennst du ein Lehrn-Übungsbuch,wo solche Aufgaben drin stehen?
Die Lösung für Differenzialgleichungen findet man im Mathe-Formelbuch,was man privat in jeden Buchladen bekommt.