Wie lässt sich die zahlenreihe fortsetzen?
Muss am dienstag zu einem einstellungstest und ich kapier nicht, wie ich von 14 auf 27 komme, aber wie ich von 13 auf 26 komme. Die aufgabe lautet:
Wie wird die Zahlenreihe fortgesetzt?
Reihe: 13 14 13 26 27 26 52
5 Antworten
Die Zahlenfolge kann ohne Randbedingungen unendlich verschieden fortgesetzt werden!
Folge aB[] für Tests ohne Hilfsmittel: einfachste aber wechselnde Grundrechenarten (in der Physik nicht zu finden, da Knicke keine saubere Ableitung ergeben).
Folge aC[] für weiche Polynom-Kurve, die man auch sauber ableiten kann (z.B. in der Physik)
Folge aD[] für Zahlentheoretiker: Nachkommastellen irrationaler Zahlen. (3510025*PI/4765098-1)/10 je 2 Nachkommastellen
Alle 3 Folgen leicht per Iterationsrechner (google erste Fundstelle) berechenbar:
siehe Bild
Tipp: schaue Dir die Differenzen und Quotienten 2er benachbarter Glieder an.
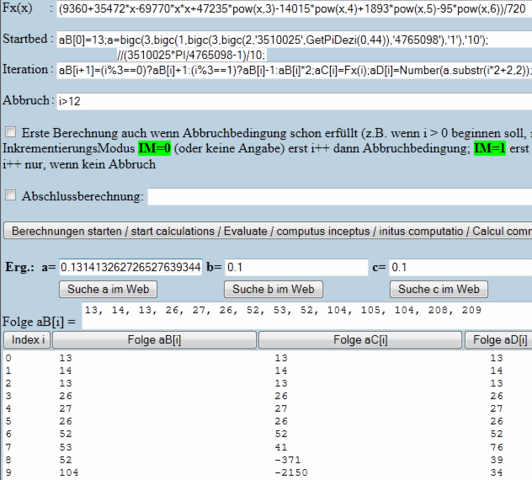
Du hast immer +1 ; -1 ; *2 ; +1 ; -1 ; *2
Also müsste dann als nächstes 53 52 104 stehen :)
13 +1 - 1 x 2 +1 -1 x 2 ... etc. es geht weiter mit 53 ; 52 ; 104 ; 105 ; 104 ; 208 etc.
plus eins, minus eins, plus "die zahl" (13) plus eins, minus eins, plus die "zahl"(26) plus eins (53) usw.
13 14 13 26 27 26 52 53 52 104 105 104 208 209 208 416 417 416... (nicht bei jeder "Zahlenreihe" muss sich die nächste Zahl immer mit der gleichen Vorschrift aus den Vorgängern ergeben, hier wechselt sich "+1", "-1" und "x2" ab...