Wie groß ist der Winkel Alpha - Vermessungstechnik?
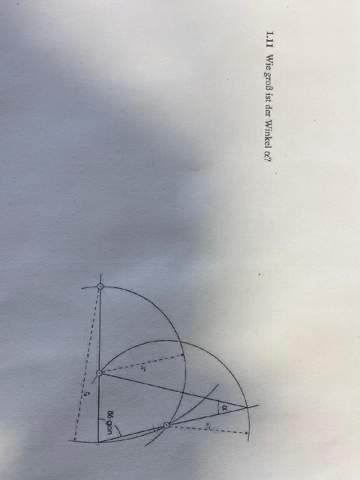
Hallo kann mir einer hierbei helfen? Komme da absolut nicht weiter und mein Aufgabensteller im Praktikum hat nur die Lösung und kein Lösungsweg. (28 gon) Eingezeichnet bestätigt sich das also muss es rechnerisch lösbar sein.
(Im Internet gibt es einen Umrechner von Gon auf Grad ;-) )
Außerdem muss es von den drei Kreisen abhängig sein. Vielleicht etwas mit einem gleichschenkligen Dreieck??
LG Niko :-)
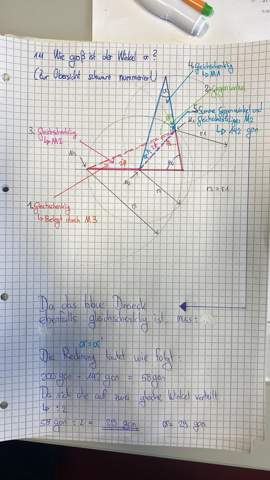
Hier die Lösung. Vielen Dank für die Hilfe 😊
3 Antworten
(Den Umrechner brauchst du nicht, wenn du konsequent in gon rechnest. Z. B. ist die Winkelsumme im Dreieck 200 gon.)
Ich würde den Punkten erst einmal Namen geben:
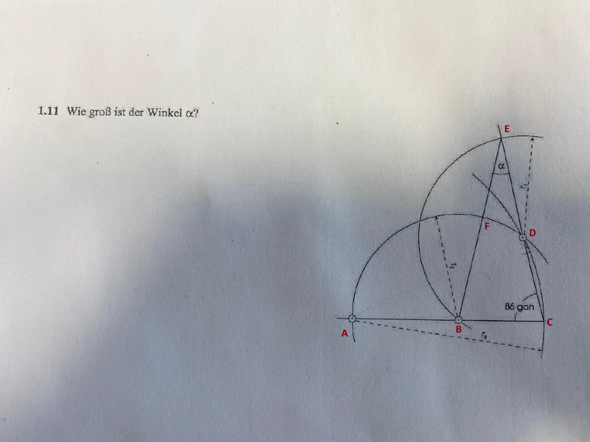
Dann hast du 20 Dreiecke mit diesen Punkten, von denen einige "entartet" sind.
Für jedes nichtentartete Dreieck kannst du die Gleichung für die Winkelsumme aufstellen.
Für jedes entartete Dreieck bzw. jeden Punkt, der eine gegebene Strecke unterteilt, kannst du für jeden Punkt, der nicht auf dieser Strecke liegt, ebenfalls eine Winkelsumme bilden. Beispiel für Punkt D, der auf Strecke(C,E) liegt:
200 gon = Winkel(A,D,C) + Winkel(A,D,E)
200 gon = Winkel(B,D,C) + Winkel(B,D,E)
200 gon = Winkel(F,D,C) + Winkel(F,D,E)
Beachte auch, dass einige der Dreiecke gleichschenklig sind, womit du weitere Gleichungen für die Winkel erhältst.
Auch sind einige Winkel wegen der gestreckten Winkel gleich:
Winkel(A,C,D) = Winkel(A,C,E) = Winkel(B,C,D) = Winkel(B,C,E)
Aus diesem Gleichungssystem und dem gegebenen Winkel(BCD) müsste sich der gesuchte Winkel(B,E,C) berechnen lassen.
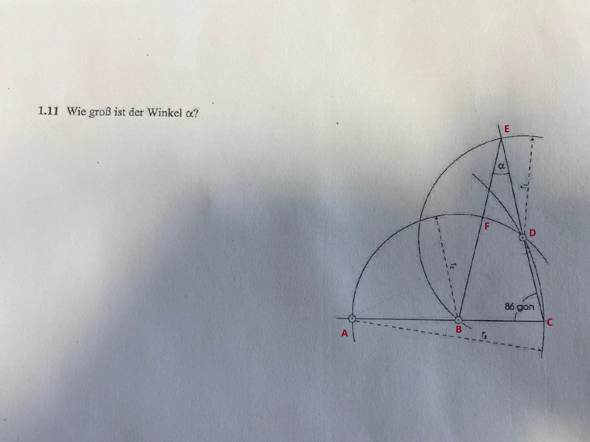
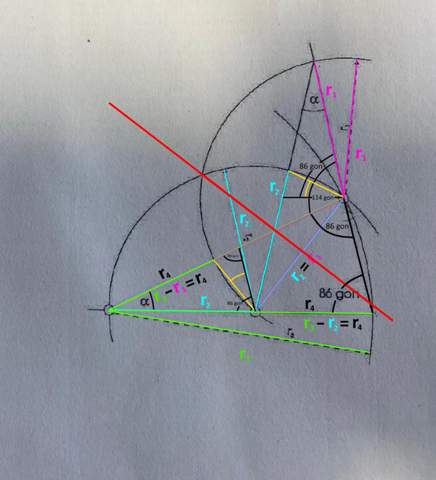
Wir sehen die Achsensymmetrie (zur roten Gerade). Da man beim Dreieck, wo die grünen Farben vorhanden sind, beweisen kann, dass es gleichschenklig ist, muss es aus Symmetriegründen auf für das vorgezeichnete gelten.
Jetzt muss man nur noch rechnen. Da die Winkelsumme in einem Dreieck 180° bzw. 200 gon beträgt und dieses gleichschenklig ist (also zwei Seiten und die zwei zu den Seiten passenden Winkel gleich sind), müssen wir von diesen 200 gon nur noch die anderen beiden (gleichen) Winkel abziehen und haben unseren Winkel Alpha.
Ich hoffe, ich konnte helfen :)
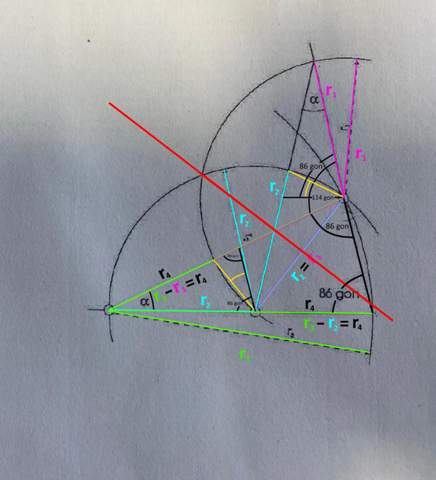
Hast vollkommen Recht.
Denke, dass der Schritt mit der Symmetrieachse bei mir falsch war.
Aber respekt, dass Du es noch geschafft hast - also nicht nur dass Du zur richtigen Lösung gekommen bist, sondern auch dieser nachvollziehbare Rechenweg.
Dein "Chef" kann stolz auf Dich sein :)
Dankeschön :-) Ja das war mir persönlich auch solch ein Dorn im Auge. Mein Vorgesetzter meinte schon, dass ich es sein lassen kann wenn ich will weil er es selbst nicht wusste. Dann ist das schon ein Erfolgserlebnis. Besonders wenn man sowieso nicht so gut in Mathe ist ;-)
Die Umrechnungsformel von gon (Neugrad) nach Grad (Altgrad) lautet:
a = gon * 360 / 400
Das hat mit der Umrechnung von gon nach Grad nichts zu tun. Man rechnet ja lediglich in eine neue Einheit um.
Und hat jetzt mit der Lösung der Aufgabe ebenfalls nichts zu tun.
Hallo vielen Dank für die Hilfe. Aber mit viel Kopfzerbrechen bekam ich es doch noch hin und habe die selbe Lösung wie in der Musterlösung ;-)
Dein Ergebnis ist leider falsch. Weil der Winkel 29 gon beträgt. 😉 Lade mein Ergebnis gleich hoch falls das geht.
Trotzdem vielen Dank :-)