Unlösbares Mathematisches Rätsel?
Kürzlich habe ich auf einer Webseite ein Rätsel gesehen welches ich im unteren Bild zeige. Kann es jemand von Ihnen lösen?
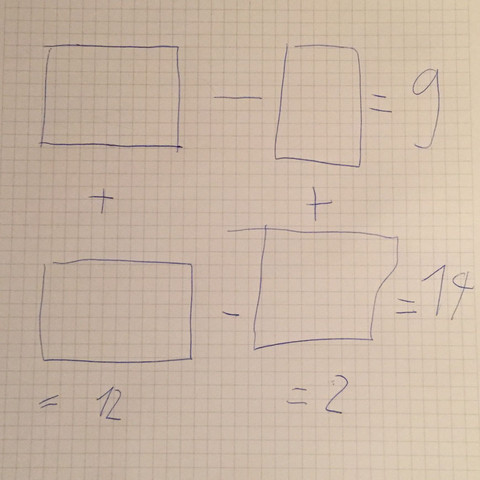
4 Antworten
Ich habs jetzt ewig probiert und kriegs auch nicht gebacken. Immer eine Zahl zu hoch.
Würde + - nicht - ergeben, würde es aber glaube ich gehen.
Machen wir mal ein Gleichungssystem daraus:
a-b = 9 I.
c-d = 14 II.
a+c = 12 III.
b+d = 2 IV.
I. → a = 9+b
in III. → (9+b)+c = 12
b = 3-c
in IV. → (3-c)+d = 2
1+d = c
in II. → (1+d)-d = 14
1 = 14
Das geht nicht, also ist die Aufgabe nicht lösbar.
Wenn Du den Zahlenbereich auf die negativen Zahlen erweiterst, dann ist es lösbar.
Da hilft nur rumprobieren und das kann langwierig sein, bis man eine mögliche Lösung hat.
Mit Erweitern geht hier nix. Wenn man den Zahlenbereich auf Z/13Z reduziert, hat man dann ne Lösung.
Restklassenring modulo 13, kann man auch Z/(13), Z/13 oder Z_13 schreiben. In dem Fall sogar Restklassenkörper F_13, da 13 prim ist.
Habe ich auch schon versucht. Schaffe es trotzdem nicht!