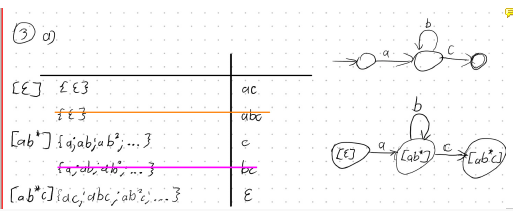
reguläre Sprachen epsilon als eigene Äquivalenzklasse?
Wie viele Äquivalenzklassen dieser regulären Sprache gibt es, die Lösung ist nachfolgend angegeben.
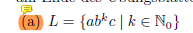
Lösung:
Wie man sieht gibt es hier genau 3 Äquivalenzklassen.
Was mich verwundert ist, warum man hier epsilon selbst als Äquivalenzklasse berücksichtigt? epsi mit Präfix ac steht doch nicht in Relation zu epsi mit präfix abc oder epsi mit Präfix abbc ...?
Anderes Bsp. Sprache ist wieder regulär

....
Es gibt unendlich viele Äquivalenzklassen. Soweit klar!
Warum berücksichtig man jetzt hier in dem Bsp. nicht epsilon selbst als Äquivalenzklasse, wie in dem Bsp. zuvor
epsi + Präfix ab oder epsi + Präfix aabb oder epsi + Präfix aaabbb...
Kann mir dies bitte jemand erklären. Danke!
3 Antworten
Das erste Beispiel hat streng genommen 4 Äquivalenzklassen. Dass ihr die vierte Klasse nicht betrachtet, hat wohl mit eurer Anschauung der Automaten zu tun. Streng genommen fehlt da nämlich noch ein Zustand, der Fehlerzustand. In diesem landet man, wenn man ein Wort hat, welches unmöglich zu einem Wort der Sprache ergänzt werden kann. In diesem Beispiel wäre da beispielsweise das b oder c drin. Das ergibt sich auch von allein, wenn man die Bedingung stellt, dass jeder Zustandsübergang für jedes Zeichen definiert werden muss.
Man nennt das einen impliziten Fehlerzustand. Man denkt sich ihn dann ggf. einfach dazu.
Epsilon selber stellt eine eigene Klasse dar, da es mit keinem anderen Wort die Nerode-Äquivalenz erfüllt. Du kannst dir ja mal überlegen: Mit welchem Präfix x ist das Wort: xab*c in der Sprache?
Epsilon hat nicht immer eine "eigene" Äquivalenzklasse. Sprachen, welche selbst Epsilon enthalten, sind eine typische Ausnahme. a* über dem Alphabet {a, b} hat beispielsweise nur die Klassen {Ɛ, a, aa, ...} und {b, ab, ba, bb, aab, ...}.
Aber auch in Beispiel 2 hat Epsilon eine eigene Äquivlanezklasse.
Mit a* meine ich hier als RegEx, also die Sprache {Ɛ, a, aa, aaa, ...}.
Intuitiv lässt sich das recht leicht überlegen. Entweder ein Wort besteht nur aus a's (oder Epsilon), dann kann ich es mit weiteren a's (oder Epsilon) zu einem Wort der Sprache ergänzen. Oder Ein Wort besteht nicht nur aus a's (enthält mindestens ein b), dann kann ich es gar nicht ergänzen.
D. h.
Sprache a* ist nicht regulär, da es unendlich viele Äquivalenzklassen gibt
=> Warum gibt jetzt hier keine "eigene" Äquivalenzklasse epsilon? gemäß Myhill-Neruode, gemäß deiner Aussage!
Moment, also wie ich sagte gibt es zwei Äquivalenzklassen. Äquivalenzklassen sind im Prinzip Mengen. Es gibt hier nur zwei Klassen, welche beide unendlich viele Wörter enthalten.
Epsilon ist hier in der ersten Klasse enthalten, welche ich aufgezählt habe. In jedem Fall ist jedes Wort in irgendeiner Klasse, auch Epsilon. Ich nehme mal an, dass du mit "eigene Klasse" meinst, dass eine Klasse nur Epsilon enthält. Das ist hier nicht der Fall, da man Epsilon, genau wie jedes andere Wort aus der Sprache, durch weitere a's ergänzen kann, sodass es (immer noch) in der Sprache liegt.
Ok, es gibt unendlich viele Äquivalenzklassen bei a* fertig.
Und wie ist es bei der Sprache ba*
{ b, ba, baa, baaa....} mit Präfix a sind alles Wörter der Sprache
{b, ba, baa, baaa...} mit Präfix aa sind auch alles Wörter der Sprache. Da Äquivalenzklassen im Prinzip Mengen sind, gibt es keine doppelten Elemente
Also liegt hier nur 1 ÄK statt 2 ÄK vor.
Was ist jetzt hier mit Epsilon als eigener ÄK? Bildet epslion jetzt hier eine eigene Äquivalenzklasse für die Sprache ba*? Ja oder Nein und Warum?
Im Prinzip könnte ich doch sagen:
{epsi} mit Präfix b
{epsi} mit Präfix ba
{espi} mit Präfix baa.... baaa....
Somit habe ich eine Äquivalenzklasse epsi die nur aus epsi selbst besteht?
Ich weiß nicht, ob wir hier aneinander vorbeischreiben (...reden)
Mir geht es einfach darum:
Wann stellt epsilon eine eigene Äquivalenzklasse bzgl. der Myhill-Neurode Relation dar und wann nicht? Einfaches Bsp. ist vollkommend ausreichend.
Ok, es gibt unendlich viele Äquivalenzklassen bei a* fertig.
Nein, es gibt genau 2, {Ɛ, a, aa, ...} und {b, ab, ba, bb, aab, ...}. a* ist regulär, es kann ja auch durch einen regulären Ausruck dargestellt werden.
Somit habe ich eine Äquivalenzklasse epsi die nur aus epsi selbst besteht?
Genau.
Wann stellt epsilon eine eigene Äquivalenzklasse bzgl. der Myhill-Neurode Relation dar und wann nicht? Einfaches Bsp. ist vollkommend ausreichend.
So allgemein ist es eben leider schwierig zu sagen. Ich würde mir einfach anschauen, ob es für Epsilon einen Suffix gibt, welcher für die anderen Äquivalenzklassen nicht funktioniert. was handlicheres fällt mir auf die Schnelle leider nicht ein.
Dein Bsp. war Alphabet {a, b} du hast jetzt einen Regex derart a*
d. h. eine beliebige Aneinanderkettung von as und bs
epsi, a, aa, b, ba, bb, bbba, ....
Deiner Aussage nach gibt es hier jetzt genau zwei Äquivalenzklassen. Richtig? Und epsilon stellt keine eigene Äquivalenzklasse für sich dar.
Das war wohl wirklich etwas missverständlich, sorry. Aber a* ist die Sprache: {a^k | k Element von N}. Über dem Alphabet {a, b} bedeutet nur, dass b's verwendet werden können, aber nicht, dass diese auch vorkommen.
Was du meinst, wäre die Sprache {a, b}*. Diese hat nur eine Äquivalenzklasse, nämlich ganz {a, b}*.
Zwei wörter x, y sind genau dann Inder selben Klasse bezüglich der Myhill-Nerode relation, wenn für jedes Wort z gilt, dass xz genau dann in der Sprache ist, wenn yz in der Sprache ist.
Epsilon ist in keiner der beiden anderen anderen Klassen, weswegen es als Repräsentant einer dritten Klasse sein muss.
Und es werden alle Klassen benötigt, für die es mindestens ein Suffix gibt, welches zu einem akzeptierenden Zustand führt, um damit dann den minimalen Automaten bilden zu können.
Anderes Bsp. Sprache ist wieder regulär
Nein ist sie nicht. Das sieht man daran, dass die Sprache unendlich viele Aquivalenzklassen hat.
Warum berücksichtig man jetzt hier in dem Bsp. nicht epsilon selbst als Äquivalenzklasse, wie in dem Bsp. zuvor
Das ist so oder so keine vollständige Auflistung, da die Klasse a, die Klasse aa, die Klasse usw fehlt.
Unters Bsp. Sprache ist nicht regulär, da hast du natürlich recht, da es unendlich viele Äquivalenzklassen gibt.
Nochmal zum ersten Bsp., wo epsilon eine Äquivalenzklasse darstellt:
Laut deiner Antwort:
"Epsilon ist in keiner der beiden anderen anderen Klassen, weswegen es als Repräsentant einer dritten Klasse sein muss."
=> Epsilon stellt somit immer eine eigene Äquivalenzklasse bzgl. der Myhill-Nerode relation dar?
=> Das im ersten Bsp. (a) k element N0 ist hat damit nichts zu tun. Es gibt immer eine Äquivalenzklasse epsilon bzgl. der Myhill-Nerode relation?
Epsilon stellt somit immer eine eigene Äquivalenzklasse bzgl. der Myhill-Nerode relation dar?
Bei einer Äqivalenzrelation muss jedes Element zu exakt einer Klasse gehören. Also muss Epsilon auch zu einer Klasse gehören. Also ja
Nochmal Rückfrage zum zweiten Bsp.
L = {a^nb^n | n ist Element IN+} d. h. die natürlichen Zahlen ohne die 0
Folgende Wörter sind Element der Sprache ab, aabb, aaabbb usw.
Ich weiß es gibt unendlich viele Äquivalenzklassen, somit ist die Sprache nicht regulär. Auch hier stellt epsilon wieder eine Äquivalenzklasse dar. Richtig?
Epsilon ist ein Repräsentant einer Äquivalenzklasse, ja. Hier gilt sogar, dass Epsilon mit keinem element in relation steht, weswegen die Klasse Epsilon genau ein Element enthält. Es gibt auch Sprachen, da hat die Klasse Epsilon auch andere Elemente, da Epsilon dann auch in relation zu anderen Elementen ist.
Gibt es auch Sprachen bzgl. Myhill-Neurode, wo epsilon keine eigene Äquivalenzklasse darstellt? Was sind hierfür typische Beispiele:
Man kann Epsilon auch berücksichtigen, aber hat man halt nicht gemacht, soweit ich das sehe.
Den impliziten Fehlerzustand lassen wir bitte weg. Den brauchen wir bei uns bzgl. den Äquivalenzklassen nicht.
Mit welchem Präfix x ist das Wort: xab*c in der Sprache? Nur mit epsilon
=> Also stellt hier epsilon eine eigene Äquivalenzklasse dar! Ok.
"Epsilon hat nicht immer eine "eigene" Äquivalenzklasse. Sprachen, welche selbst Epsilon enthalten, sind eine typische Ausnahme. a* über dem Alphabet {a, b} hat beispielsweise nur die Klassen {Ɛ, a, aa, ...} und {b, ab, ba, bb, aab, ...}"
=> Mit a* meinst du hier sicherlich eine beliebige Reihenfolge aus dem Alphabet {a,b}. {Ɛ, a, aa, ...} espsi liegt hier mit drinnen klar.
Warum gibt es jetzt hier nur zwei Äquivalenzklassen? Verstehe ich nicht.