Mathe?
Wie hoch kann der Schrank sein?
60 cm breit
(Geht das ohne die stufen zu betrachten)
Kann das jmd ausrechnen?
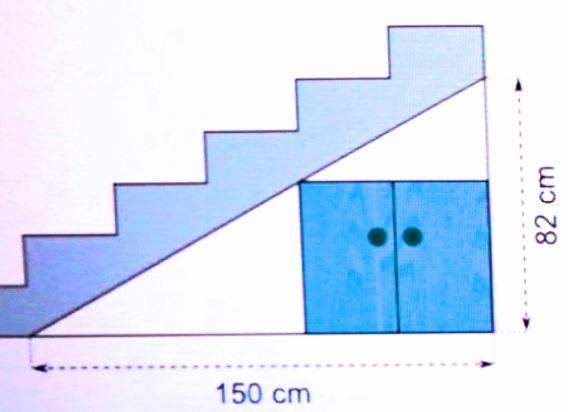
.
4 Antworten
Also die einfachste Lösung ist hier wohl tatsächlich eine einfache Gleichung.
Am Ende der Treppe, also nach 150cm ist der Raum 82cm hoch. Am Anfang der Treppe, also nach 0cm ist die Höhe unter der Treppe 0cm, sie liegt ja dem Boden auf. Nun soll die Treppe kontinuierlich auf einer Strecke von 150cm bis auf 82cm ansteigen. Da der Anstieg kontinuierlich ist, hat ist die Treppe bei der Hälfte der Strecke auch schon bis zur Hälfte der Zielhöhe angestiegen. Bei zwei Drittel der Strecke hat sie schon zwei Drittel der Höhe erreicht.
Bei Der Schrank 60m breit und soll offenbar unter der Treppe stehen. Er nimmt also die letzten 60cm der 150cm-Gesamtstrecke ein, die Seitenwand des Schrankes wird also bei 90cm der Gesamtstrecke stehen.
Es verhält sich also die Strecke bis zur Schrankwand zur Gesamtstrecke , so wie gesuchte Schrankhöhe zur Maximalhöhe. Das ist letztlich der so genannte "Strahlensatz".
Die Gleichung sieht dann wie folgt aus:
(150 - 60)cm / 150cm = X / 82cm
Das lösen wir langsam, Schritt für Schritt nach X auf:
Erstmal Brüche auflösen.
90cm/150cm = X /82cm
0,6 = X / 82cm
0,6*82cm = X
49,2cm = X
Der Schrank darf also maximal 49,2cm hoch sein, wenn er unter die Treppe passen soll.
Das kommt mir zwar als ein sehr krummes Ergebnis vor, aber wird wohl auch nicht gerade die Grundschule sein.
Berechne die Höhe der Treppenunterseite bei 90cm.
Dreisatz, Strahlensatz, Funktionswerte... Viele Wege führen nach Rom.
Ja, macht man mit Verhältnissen.
bla zu blub verhält sich wie pieep zu pup
und dann löst man nach dem gesuchten auf
150 zu 82 sind wie 90 zu der gesuchten höhe
Also ich kann es
Wieviel ist das jetzt?