Lineare Funktionen - ohne Nullstellen?
Gibt es lineare Funktionen die keine Nullstellen besitze?
11 Antworten
f(x)=x+0
es ist egal welche zahl vor x steht, hauptsache n=0
Würden sie keine Nullstelle besitzen, müsste sie zwangsläufig parallel zur x-Achse verlaufen. Dann ist es jedoch noch immer eine Funktion, da die Definition ja lautet, dass sie höchstens einen y-Wert pro x-Stelle zugeordnet haben dürfen. Daher handelt es sich tatsächlich um eine Funktion, die keine Nullstelle besitzt.
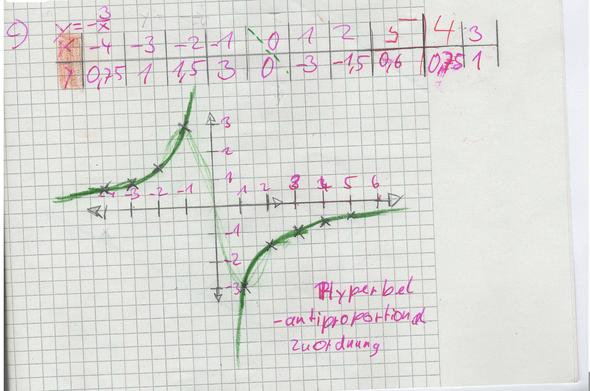
Wenn da steht z.B. wir hatten am anfang da stehen y=-3:x und dann hatten wir eine tabelle mit den x werten und ein x wert war 0 aber man nicht durch 0 teilen darf muss man diesen ausslassen und wenn man das jetzt und endlich groß zeichnet (den Graph) er wird nie über die y-Achse gehen also würde bei x z.B. immr sowas wie 0,0000000000000001 rauskomme. Ich sende auch gleich mak ein Bild hinten dran dann Kannst du es dir anschauhen ;-)
Hoffe ich konnte helfen Smily219
ja, y(x) = ax + b besitzt keine Nullstelle, wenn
1) a = 0 und b ungleich 0
2) die Urbildmenge das Element -b/a nicht enthält
Nein, gibt es nicht. f(x) = c ist nach Definition keine Lineare Funktion, sondern eine Konstante. (Lineare Funktion = ax+b für a ungleich 0)