Kann mir jemand bei der mathe aufgabe helfen habe ich was falsch gemacht?
Es geht um strahlensätze . Die nr 5 . gelöst habe ich sie aber ich bin mir nicht sicher ob mein ergebnis richtig ist weil ich zwei verschiedene ergebnisse habe
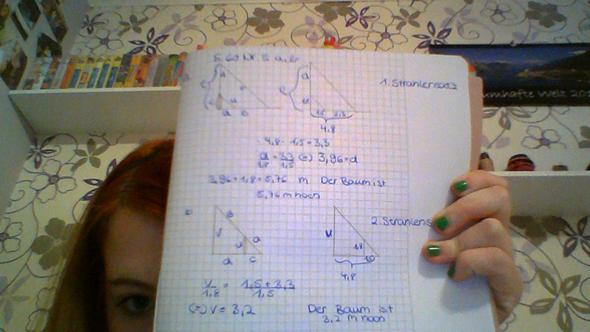
Die aufgabe ist Ein baum wirft einen schatten von 4,8 m . die daneben stehende person von 1,8 m größe wirft einen schatten von 1,5 m . wie groß ist der baum?
bei a ist der baum e und bei b v
3 Antworten
Wenn ich das richtig sehe, hast du da einen Strich gemalt - das soll jetzt der Baum sein! - mit einer Höhe X - dazu eine Grundlinie (das soll jetzt die Schattenlänge sein . 4,8 m. - Und dann noch den (gerade noch fehlenden) Sonnenstrahl, der eben noch die Baumspitze trifft - und die Linie, die er bis zum Boden entlangspazieren würde, wäre er nicht um 1 Lichtstrahldicke zu tief 'geflogen'. Ist aber egal: jede mm-Einteilung eines Maßbandes ist viel zu grob - und so genau wollen wir's ja auch nicht wissen, nur auf dm genau.
Und dann steht da noch dat Männeken - (so'n kleiner Strich); hat sich genau so aufgebaut, dass seinen Schattenlänge genau am Baumschattenende - äh, ja, endet. - Also 1,8 m hoch, 1,5 m bodenlang. - Korrekt! - Da kannst du jetzt den Strahlensatz 'anwenden' (bzw. muss, is ja gerade dran). Der drückt ja auch nichts anderes aus als: das Verhältnis von Höhe und Schattenlänge ist gleich - 'übersetzt' (in mathematische Schreibweise) X:4,5 = 1,8:1,5. Bequemerweise ergibt sich daraus eine Gleichung, die nur nur noch ausrechnen musst. Du kannst aber auch aus 1,8:1,5 den Faktor 1,2 bestimmen, um den der Baum seine Schattnlänge überragt. Oft gibt's mehrere Wege - nur muss dann das Ergebnis jeweils gleich sein.
Hast du verschiedene Ergebnisse: dann nehm' dir das falsche vor und stelle fest, wo der Fehler ist - und dann: warum? - Warum hast du da falsch gedacht? Oder war's Flüchtigkeit? - Schätze mal:hast du Fehlerort- und Ursache gefunden: dann hast du richtig was gelernt!
Du rechnest erstmal den Winkel aus, den der Strahl mit dem 1,8 Meter großen Mann bildet. Das geht, denn da gibt es einen 90-Gradwinkel und zwei Seiten eines Dreiecks, welche 1,5 und 1,8 lauten. Diesen Winkel kannst dann bei dem Baum einsetzen und hast neben dem 90-Grad-Winkel noch die 4,8-Meter-Seite. Damit lässt sich die Höhe es Baumes errechnen.
Man braucht keine Strahlensätze auswendig lernen. Man muss nur Dreiecksberechnungen beherrschen und wissen, dass man bei 3 gegebenen Angaben eines Dreiecks alle anderen ausrechnen kann. Und bei rechtwinkligen Dreiecken ist das besonders einfach. Nicht nur, weil eine Angabe schon frei Haus gegeben ist: der 90-Grad-Winkel.
Sers
Pacjam
Ich halte es für sehr sinnvoll, das Denken in Proporationalitäten zu lernen, für das Strahlensätze eine passende geometrische Veranschaulichung sind.
Mit "Auswendiglernen" hat das nach meinem Empfinden recht wenig zu tun, dafür viel mit einem Grundverständnis von "Verhältnismäßigkeit", im mathematischen wie im außermathematischen Sinne. Die Lösung elumanias ist da vorbildlich.
psychironiker
Der Baum ist 5,76m hoch.
x / 4,80 = 1,80 / 1,50
x= 5,76m