Hilfe! Schwere Mathe-Aufgabe?
Ich brauche dringend eure Hilfe.
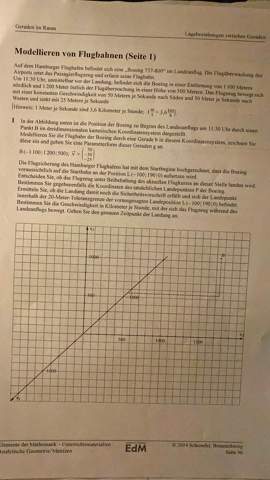
Diese Mathe-Aufgabe brauche ich bis Morgen:
Eine Freundin und ich kommen nicht voran und das seit zwei Stunden!
Wäre jemand so lieb? :(
1 Antwort
Zuerst einmal sollt ihr ja den Flugkurs einzeichnen. Der Startpunkt B der Beobachtung ist schon eingezeichnet, fehlt nur noch der Richtungsvektor...
Wie ihr an den Einheiteneinteilungen erkennen könnt, entspricht ein diagonales Kästchen auf der x1-Achse 200 Einheiten, in x2- und x3-Richtung entspricht eine Kästchenbreite/-höhe 100 Einheiten. Ihr müsst nun von Punkt B aus den Vektor (50 -50 -25) abtragen. Nur sind diese Einheiten in den entsprechenden Richtungen bei diesen Achseneinteilungen äußerst ungenau. Da es von B aus aber mit "allen möglichen" Vielfachen dieses Vektors weggeht, macht es für den nächsten Punkt Sinn diesen Vektor mit 2 zu multiplizieren, d. h. ihr geht von B aus den Vektor (100 -100 -50) weiter, also ein halbes diagonales Kästchen nach vorne links in x1-Richtung, dann ein Kästchen nach links und ein halbes nach unten. Durch diesen zweiten Punkt zieht ihr dann die Gerade von B aus durch.
Die Geradengleichung lautet "einfach":
g: x=(-1100 1200 500) + r (50 -50 -25)
Jetzt müsst ihr prüfen, ob L ein Punkt dieser Geraden ist, also die Geradengleichung mit L gleichsetzen und für jede der 3 Koordinaten eine eigene Gleichung aufstellen und jeweils nach r auflösen. Kommt bei allen das gleiche r raus, dann liegt L auf dieser Geraden, was hier aber nicht der Fall sein wird...
Um den tatsächlichen Landepunkt P zu ermitteln, müsst ihr die x3-Koordinate der Geradengleichung gleich Null setzen und das r ermitteln. Dieses r dann in g einsetzen und so den tatsächlichen Landepunkt P ermitteln.
Zuletzt muss nun noch die Entfernung zwischen L und P ermittelt werden, d. h. ihr müsst die Länge der Geraden L-P (oder P-L, das ist natürlich egal) ermitteln und prüfen, ob diese Länge (ist in Metern) innerhalb der 20m-Toleranz liegt.
