Hexadezimalsystem reste?
Moin, ich versteh das berechnen von dez zu hex nicht...
in dem Video sagt er 23 283 / 16 = 1455 rest 3???
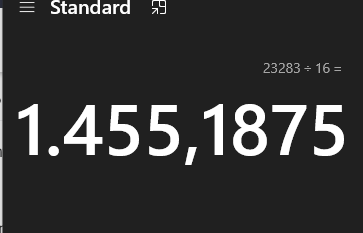
wenn ich das in meinem rechner eingebe, dann kommt 1455,18 raus? was versteh ich hier nicht
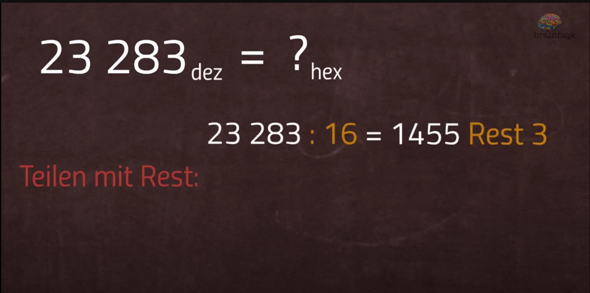
3 Antworten
Die Taschenrechner rechnen mit Dezimalbrüchen. Man muss also das, was hinter dem Komma steht, wieder mit 16 multiplizieren, da kommt dann 3 raus.
Dann lässt man den Rest weg und wiederholt das Spiel mit der 1455.
Du kannst beim Teilen eine Aufgabe auch zeichnerisch lösen, so wie es oft in der ersten oder zweiten Klasse gemacht wird, das man Äpfel zeichnet und die Gruppiert. Du hast also 17 Äpfel und willst das durch 5 teilen, da machst Du einfach Gruppen von jeweils 5 Äpfeln, und die restlichen Äpfel sind der Rest, hier 2. Wenn Du das jedoch in einen Taschenrechner eingibst, kommt 3,4 raus. Jetzt kannst Du, um auf den Rest zu kommen, theoretisch die Stellen hinterm Komma nehmen und die mit der 5. Bestimmt gibt es auch ne Methode wie man da jetzt direkt drauf kommt, aber so beschäftigt hab ich mich das letzte mal in der 2. Klasse mit Resten und sowas.
Der Rest sind nicht die Nachkommastellen.
3/16=0,1875
Ich benutze eine andere Methode zur Umrechnung vom Dezimalsystem ins Hexadezimalsystem, die einen Taschenrechner mit Logarithmus erfordert.
Darf ich sie dir erklären?
natürlich, ich nehm alle tipps für die morgige klausur an ^^
Das würde mich auch interessieren. 😉
Ich kenne zwar mehrere Methoden zur Umrechnung zwischen Zahlensystemen, aber was mit Logarithmen war da noch nicht dabei.
Erstmal: Weißt du, was die Basis, der Exponent und ein Logarithmus ist?
Dann fügst du die einzelnen Minuenden von oben nach unten zu einer Hexadezimalzahl ztusammen, wobei A=10, B=11, C=12, D=13, E=14 und F=15 ist.
Das wäre mein Rechenweg:
23283
log(16,23283) ergibt abgerundet 3
5*16^3
2803
log(16,1803) ergibt abgerundet 2
10*16^2
243
log(16,243) ergibt abgerundet 1
15*16^1
3
log(16,3) ergibt abgerundet 0
3*16^0
5AF3
Als Erstes musst du den Logarithmus der Basis des Zahlensystems, in das du umrechnen willst, von der Zahl, die du umrechnen willst, nehmen und das Ergebnis abrunden. Dann teilst du deine Zahl durch die Basis des Zahlensystems, in das du umrechnen willst, potenziert mit dem ersten abgerundeten Ergebnis. Was dabei herauskommt, musst du abrunden. Nun schreibst du das abgerundete Ergebnis multipliziert mit der Basis des Zahlensystems, in das du umrechnen willst, potenziert mit dem ersten abgerundeten Ergebnis. Das ziehst du dann von der Zahl im Dezimalsystem, die du umrechnen willst, ab. Diese Schritte wiederholst du mit der Differenz solange, bis du letztendlich bei einer Differenz von 0 angekommen bist.