Gleichmäßig beschleunigte Bewegung (Frage zu einem Experiment)?

2 Antworten
Hallo ThelittlesacxX,
eine gleichmäßige Beschleunigung ist der Fall natürlich nur in guter Näherung, wenn
- die Fallhöhe auf jeden Fall viel kleiner ist als der Erdradius (da die Gravitations-Feldstärke entfernungsabhängig ist¹)), und
- der Einfluss von Statischem Auftrieb²) und Luftwiderstand klein gehalten werden (s. Frage 2).
Wenn die erste Bedingung erfüllt ist, ist der Betrag der Beschleunigung im Mittel g = 9,81 m⁄s²; dies entspricht der mittleren Gravitationsfeldstärke an der Erdoberfläche. Statischer Auftrieb verringert sie²).
Zu Frage 2Der Körper sollte eine möglichst große Dichte haben und nach unten hin möglichst geformt sein.
Die Fallhöhe muss natürlich groß genug sein, um den Fall über eine hinreichend lange Strecke beobachten zu können, aber auch nicht so groß, dass die Reibungskraft (NEWTONsche Reibung) eine nennenswerte Rolle spielt. Am besten sind wohl einige Meter.
MessmethodenMeine erste Idee war die, in regelmäßigen Abständen Lichtschranken anzubringen, die bei Unterbrechung sofort die Zeit aufzeichnen. Geschwindigkeit lässt sich allerdings nur in Form einer Durchschnittsgeschwindigkeit ermitteln.
Eine genauere Messmethode ist aber die, den Fall zu filmen und den Film dann anhand der Einzelbilder (die ja einen festen Zeitabstand haben) auszuwerten. Es empfiehlt sich, dies aus größerer Entfernung mit Zoom zu machen, um perspektivische Verzerrungen zu minimieren, und eine Zeitlupenkamera zu verwenden, um viele Einzelbilder zu haben und Bewegungsunschärfe zu minimieren.
Anhand der Nummer des Einzelbildes lässt sich die Zeit ablesen, die zurückgelegte Strecke kann man auf den Einzelbildern ablesen. Das momentane Tempo lässt sich als Quotient aus Strecke und Zeitspanne zwischen zwei aufeinander folgenden Einzelbildern berechnen, und wenn man das bei der Auswertung des Films in regelmäßigen Abständen macht, kann man auch das Tempo als Funktion der Zeit darstellen.
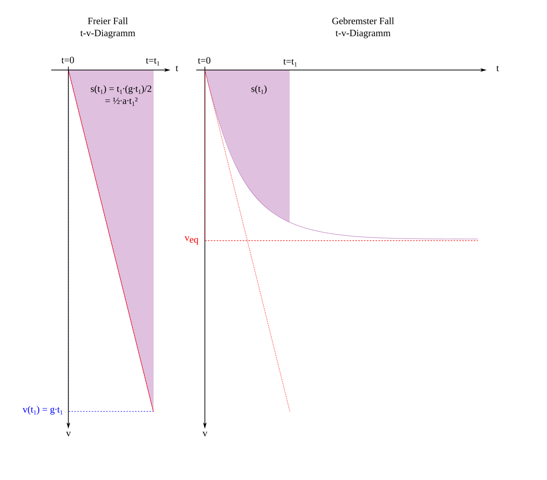
Dabei sollte eine Gerade herauskommen, ähnlich wie im Bild links. Rechts sehen wir, was passiert, wenn der Körper durch Luftreibung abgebremst wird.
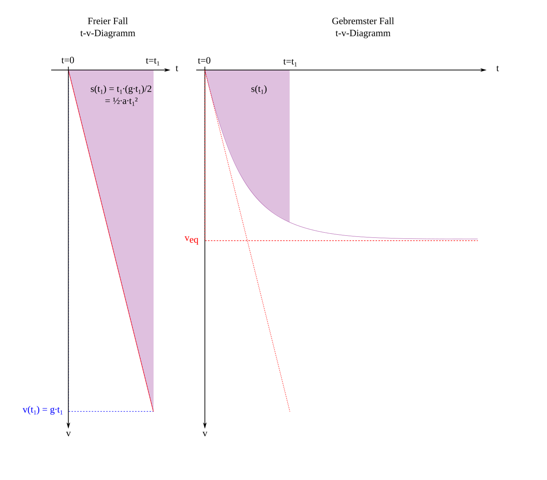
Abb. 1: Freier Fall, wenn Luftwiderstand keine Rolle spielt/ eine wesentliche Rolle spielt
¹) Abhängigkeit von der EntfernungVermutlich hast Du schon vom NEWTONschen Gravitationsgesetz gehört. Das stellt die Gravitations-Feldstärke als Funktion der Entfernung dar. Da die Richtung klar ist, brauchen wir nur die Beträge:
(1) g = GM/r²
Dabei ist G die Gravitationskonstante und M die Masse des Himmelskörpers, um den es geht, und r ist der Abstand eines Körpers vom Schwerpunkt des Himmelskörpers, wobei r ≥ R (Radius des besagten Himmelskörpers) sein sollte.
In unserem Fall ist der Himmelskörper natürlich die Erde. Mit wachsender Höhe nimmt g also ab, allerdings bei Höhen im Meter- bis Kilometerbereich unter der Nachweisgrenze.
²) Statischer AuftriebEinen Auftrieb erfährt nicht nur ein Heißluftballon, der tatsächlich aufsteigt, sondern jeder Körper. Seine Gewichtskraft verringert sich um die Gewichtskraft der Luft, die der Körper verdrängt.
Da die Trägheit dieselbe bleibt, wird ein Körper in Luft von Anfang an (also schon bevor die Reibung greift) umso geringfügiger beschleunigt, je kleiner seine Dichte ist.
Die effektive Gewichtskraft beträgt
(2.1) Feff = g∙(ρKörper − ρLuft)∙V
und die effektive Fallbeschleunigung am Anfang
(2.2) geff = g∙((ρKörper − ρLuft)/ρKörper)∙V
Bei luftgefüllten Luftballons sieht man das ganz gut. Allerdings wird bei ihnen sehr schnell die Reibung wichtig, und sie sinken nach kurzer Fallzeit nur noch. Bei Helium- gefüllten Ballons ist das noch krasser, da die effektive Gewichtskraft negativ wird.
Hey, sicher, dass das richtige Grammatik ist:
"Wenn die Bedingung ist der Betrag der Beschleunigung im Mittel g = 9,81 m⁄s²; dies entspricht der mittleren Gravitationsfeldstärke an der Erdoberfläche. Statischer Auftrieb verringert sie²).
Zu Frage 2Der Körper sollte eine möglichst große Dichte haben und nach unten hin möglichst geformt sein."
Ja, gleichmäßig
9,81 m/s²
Für den Versuch nen kleinen schweren Gegenstand nehmen, um den Einfluss des Luftwiderstandes zu minimieren. (Eine Feder aus dem Fenster werfen geht also nicht.) Fallhöhe muss hoch genug sein, um die Fallzeit einigermaßen genau ermitteln zu können. Also lieber nen Stein aus dem 10 Stock falen lassen.
Aus Fallhöhe und Fallzeit lässt sich dann auf die Erdbeschleunigung 9,81m/s² zurückrechnen, was dann wiederum beweist, dass es sich um eine gleichmäßige Beschleunigung handelt.
s=Höhe in m
g=9,81m/s²
t=Zeit in s
s=1/2g t², umstellen nach g=2s/t², sollte dann mit den ermittelten Werten 9,81m/s² ergeben.
Könntest du, wenn du Lust hast, deine Antwort weiter ausgestalten? also nicht, dass du mich falsch verstehst, ich meine nur weitere denkansätze, die dir so einfallen