Gibt es eine Zahl Null-komma-null-periode-eins?

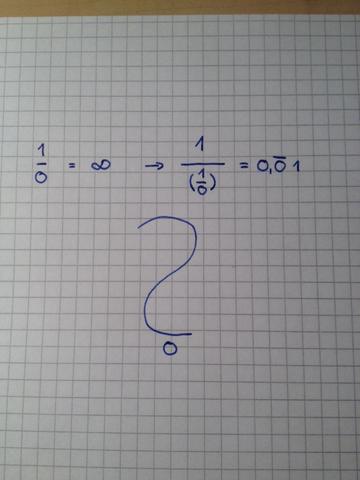
Im Bild - Existiert diese Zahl? Brauche diese Überlegung für eine asymptotische Darstellung.

Answer 1

[BistDuSicher]

Du kannst nicht einfach durch 0 dividieren und dann so tun als sei unendlich eine normale Zahl und durch das durchdividieren.

1/0 ist nicht definiert, aber man hat sich geeinigt, dass es gegen Unendlich geht. Das heißt nicht, dass es einfach so unendlich ist. Nur das der Grenzwert von etwas das gegen 0 geht divergiert. Lim(1/x) für x gegen 0 = Unendlich.

Aber selbst wenn es einfach so Unendlich wäre, würde deine Folgerung immer noch nicht gelten (1/unendlich kann man nämlich genauso wenig rechnen).

Was du ausrechnen kannst ist der Grenzwert von 1/(1/x) für x gegen 0. lim (1/(1/x))=lim(x)=0

Das heißt immer noch nicht, dass der Bruch selbst 0 ist, aber der Grenzwert, wenn du für den Nenner im Nenner gegen 0 gehst ist 0.

Comments

[BistDuSicher]

Suchst du eigentlich nach der kleinsten Zahl kleiner 0? Das geht leider bei den reelen Zahlen (und den meisten anderen) nicht...

Answer 2

[FataMorgana2010]

Nein. Überlege doch mal, was die Zahl 0,periode 0 überhaupt ist - das ist der Grenzwert der Folge

0,0

0,00

0,000

0,0000

usw.

So ist die Periode definiert. Wie soll denn der Ausdruck, den du da aufschreibst, definiert sein? Welchen mathematischen Sinn soll das haben?

Und dann zu 1/0 - auch dieser Ausdruck ist nicht definiert. Was man sagen kann, ist:

"Die Folge 1/x für x -> 0 divergiert bestimmt gegen + unendlich". Das ist aber was anderes.

Woher ich das weiß: Studium / Ausbildung – Dipl.-Math. :-)

Answer 3

[triopasi]

Teilen durch 0 geht nicht. 1/0 = undefiniert.

Comments

[FFXDesigns]

Alles klar, hat sich erledigt. Denkfehler bei mir ;D

Answer 4

[Wunderkerze2012]

1. Eine Division durch 0 ist immer undefiniert (bzw. "nicht definiert").

2. Sobald eine Periode beginnt, widerholt sich diese Zahl(enfolge) immer wieder und es kann keine andere Zahl mehr folgen.

3. Dem Titel zufolge müsste der Periodenstrick über der 1 liegen, also lieber "Null-Komma-Periode-Null-(Eins), wobei die 1 in diesem Sinne gar nicht mehr folgen kann, sonst müsste der Periodenstrich über 0 und 1 liegen! :-)

LG, Wunderkerze2012

Comments

[FFXDesigns]

Alles klar, hat sich erledigt. Denkfehler bei mir ;D

Answer 5

[claushilbig]

Nein, das was Du meinst, gibt es nicht, denn nach einer Periode kann keine andere Ziffer mehr kommen. Die Periode bedeutet ja, dass sich diese Ziffer unendlich wiederholt, es gibt also kein "dahinter" mehr.

Das, wonach Du in der Überschrift (in Worten) fragst, gibt es allerdings schon, denn das wäre 0,0111111111111111111111111111111111111... - die periodische Ziffer(nfolge) ist immer die, die nach dem Wort "Periode" genannt wird. Das ist auch sinnvoll, weil es - wie gesagt - danach ja keine anderen Ziffern mehr gibt. Die Zahl, die Du hingeschrieben hast, kann man gar nicht aussprechen