Geschwindigkeiten beim schiefen Stoß?

Hallo zusammen,

ich kenne die Theorie zum nicht zentralen Stoß, aber hier bin ich echt verloren, ich weiß das der Winkel weg en den selben Maßen 90grad sein muss, das wars. Würde mich echt über Hilfe freuen, danke :)

Answer 1

[mihisu]

„ich weiß das der Winkel weg en den selben Maßen 90grad sein muss“

„der Winkel“? Welchen Winkel meinst du?

=============

Da ich die Aufgabe jetzt einfach mal selbst durchgerechnet habe, habe ich dir einfach mal meine Lösung komplett unten aufgeschrieben, statt dir nur kleinere Hilfestellungen zu geben.

Du kannst ja mal schauen, ob du die selbst nachvollziehen kannst. Wenn du währenddessen Ideen bzw. Denkanstöße bekommst, kannst du ja einfach an geeigneter Stelle das Lesen meiner Lösung unterbrechen und selbst erst einmal deine eigenen Rechnungen durchführen.

=============

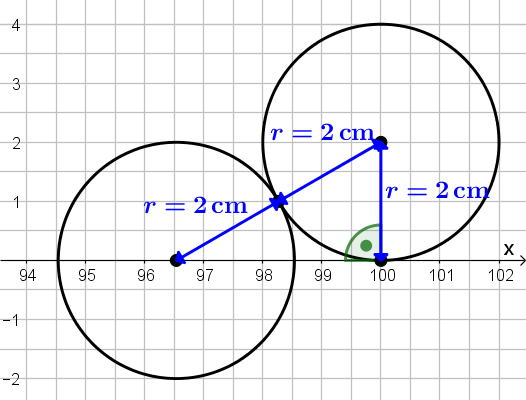
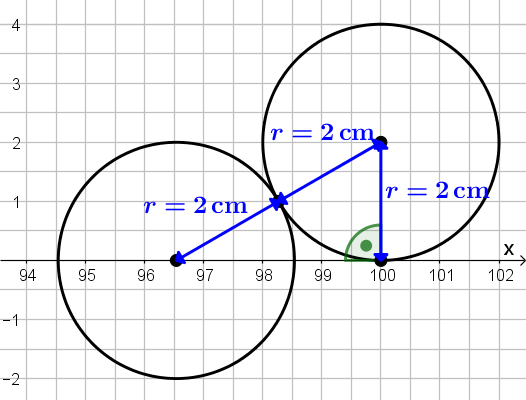
So sieht die Situation zum Zeitpunkt des Stoßes aus...

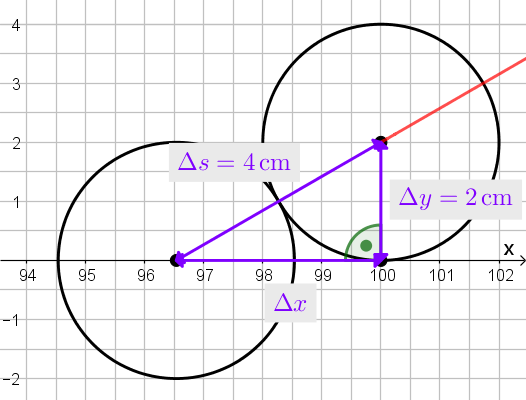
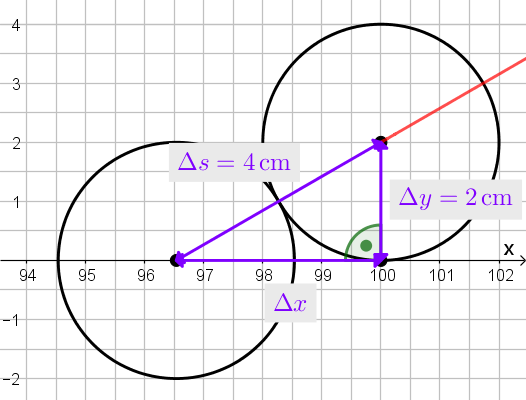
Nach dem Stoß wird sich der zweite Puck (bzw. genauer: der Schwerpunkt des zweiten Pucks) entlang der roten Geraden wegbewegen.

$\Delta s=r+r=2\cdot r$

$\Delta y=r$

Mit Satz des Pythagoras...

$\left(\Delta x\right)^2+\left(\Delta y\right)^2=\left(\Delta s\right)^2$

$\rightarrow \quad\Delta x=\sqrt{\left(\Delta s\right)^2-\left(\Delta y\right)^2}=\sqrt{\left(2\cdot r\right)^2-r^2}=\sqrt{4\cdot r^2-r^2}=\sqrt{3\cdot r^2}=\sqrt{3}\cdot r$

Wenn...

$\vec{u}_2 =u_{x2}\cdot\vec{e}_x+u_{y2}\cdot\vec{e}_y$

... die Geschwindigkeit des gestoßenen Pucks nach dem Stoß ist, so ist das Dreieck mit den Seiten u[x2], u[y2], u[2] ähnlich zum Dreieck mit den Seiten Δx, Δy, Δs. Dementsprechend erhält man insbesondere ...

$\frac{u_{y2}}{u_{x2}}=\frac{\Delta y}{\Delta x}$

Bzw. könnte man auch u[y2]/u[x2] und Δy/Δx beides als Steigung der roten Geraden sehen, und so darauf kommen. Jedenfalls erhält man daraus weiter...

$u_{y2}=\frac{\Delta y}{\Delta x}\cdot u_{x2}=\frac{r}{\sqrt{3}\cdot r}\cdot u_{x2}=\frac{1}{\sqrt{3}}\cdot u_{x2}$

Zusammen mit Impulserhaltung und Energieerhaltung erhält man dann das folgende Gleichungssystem...

$[1]:\quad \frac{1}{2}\cdot m\cdot v_{x1}^2=\frac{1}{2}\cdot m\cdot \left(u_{x1}^2+u_{y1}^2\right)+\frac{1}{2}\cdot m\cdot \left(u_{x2}^2+u_{y2}^2\right)$

$[2]:\quad m\cdot v_{x1}=m\cdot u_{x1}+m\cdot u_{x2}$

$[3]:\quad 0=m\cdot u_{y1}+m\cdot u_{y2}$

$[4]:\quad u_{y2}=\frac{1}{\sqrt{3}}\cdot u_{x2}$

Dabei ist...

• v[1] = (v[x1], 0) die Geschwindigkeit des ersten Pucks vor dem Stoß,
• u[1] = (u[x1], u[y1]) die Geschwindigkeit des ersten Pucks nach dem Stoß,
• u[2] = (u[x2], u[y2]) die Geschwindigkeit des ersten Pucks nach dem Stoß.

Dieses Gleichungssystem mit 4 Gleichungen kannst du nun bezüglich den Unbekannten u[x2], u[y2], u[x1], u[x2] lösen.

Löst man die Gleichungen [2] und [3] nach u[x1] bzw. u[y1] auf und setzt das in [1] ein, erhält man...

$\frac{1}{2}\cdot m\cdot v_{x1}^2=\frac{1}{2}\cdot m\cdot \left(\left(v_{x1}-u_{x2}\right)^2+\left(-u_{y2}\right)^2\right)+\frac{1}{2}\cdot m\cdot \left(u_{x2}^2+u_{y2}^2\right)$

$\rightarrow\quad v_{x1}^2=\left(v_{x1}-u_{x2}\right)^2+\left(-u_{y2}\right)^2+u_{x2}^2+u_{y2}^2$

$\rightarrow\quad v_{x1}^2=v_{x1}^2-2\cdot v_{x1}\cdot u_{x2}+u_{x2}^2+u_{y2}^2+u_{x2}^2+u_{y2}^2$

$\rightarrow\quad 0=-2\cdot v_{x1}\cdot u_{x2}+2\cdot u_{x2}^2+2\cdot u_{y2}^2$

$\rightarrow\quad 0=-v_{x1}\cdot u_{x2}+u_{x2}^2+u_{y2}^2$

Setzt man Gleichung [4] in diese Gleichung ein, erhält man...

$0=-v_{x1}\cdot u_{x2}+u_{x2}^2+\left(\frac{1}{\sqrt{3}}\cdot u_{x2}\right)^2$

$\rightarrow\quad 0=-v_{x1}\cdot u_{x2}+u_{x2}^2+\frac{1}{3}\cdot u_{x2}^2$

$\rightarrow\quad 0=-v_{x1}\cdot u_{x2}+\frac{4}{3}\cdot u_{x2}^2$

Da u[x2] = 0 keinen Sinn ergibt... (Bei dieser Lösung würde quasi der erste Puck durch den zweiten Puck durchtunneln, ohne dass die beiden Pucks sich gegenseitig beeinflussen.) ... kann man von u[x2] ≠ 0 ausgehen und dementsprechend bei der zuvor erhaltenen Gleichung durch u[x2] dividieren.

$\rightarrow\quad 0=-v_{x1}+\frac{4}{3}\cdot u_{x2}$

$\rightarrow\quad \frac{4}{3}\cdot u_{x2}=v_{x1}$

$\rightarrow\quad u_{x2}=\frac{3}{4}\cdot v_{x1}$

Mit der gegebenen Geschwindigkeitskomponente v[x1] = 100 cm/s erhält man...

$u_{x2}=\frac{3}{4}\cdot v_{x1}=\frac{3}{4}\cdot 100\,\frac{\text{cm}}{\text{s}}=75\,\frac{\text{cm}}{\text{s}}$

Eingesetzt in Gleichung 4 erhält man...

$u_{y2}=\frac{1}{\sqrt{3}}\cdot u_{x2}=\frac{1}{\sqrt{3}}\cdot 75\,\frac{\text{cm}}{\text{s}}\approx 43\text{,}30\,\frac{\text{cm}}{\text{s}}$

Damit hat man die Geschwindigkeit...

$\vec{u}_2= 75\,\frac{\text{cm}}{\text{s}}\cdot \vec{e}_{x}+\underbrace{\frac{1}{\sqrt{3}}\cdot 75\,\frac{\text{cm}}{\text{s}}}_{\approx 43\text{,}30\,\frac{\text{cm}}{\text{s}}}\cdot \vec{e}_{y}$

Mit den Gleichungen [2] und [3] entsprechend der Impulserhaltung erhält man dann auch die andere Geschwindigkeit...

$\vec{u}_1= 25\,\frac{\text{cm}}{\text{s}}\cdot \vec{e}_{x}-\underbrace{\frac{1}{\sqrt{3}}\cdot 75\,\frac{\text{cm}}{\text{s}}}_{\approx 43\text{,}30\,\frac{\text{cm}}{\text{s}}}\cdot \vec{e}_{y}$

Comments

[TrViMa]

Okay wow, größten Dank dir :)