Eigenfrequenz und Resonanz Physik?
Moin zusammen,
Ich habe eine Aufgabe in Physik bekommen und zwar: "Erkläre die Begriffe Eigenfrequenz und Resonanz. Erläutere, wie diese beim erdbebensicheren Bauen berücksichtigt werden können. " Ich weiß leider nicht, wie ich an diese Aufgabe herangehen soll....:( kann mir jemand helfen?
Vielen Dank!
4 Antworten
Vielleicht noch ein paar Ergänzungen, die ein wenig die Brücke von Schulphysik zu Alltag ansprechen: Ihr habt wahrscheinlich Systeme wie Fadenpendel und physikalisches Pendel kennengelernt, und wie da Schwingungsdauer und deren Kehrwert, die Frequenz, von den Eigenschaften des Pendels abhängen. Beim physikalischen Pendel hängt sie von Masse, Trägheitsmoment bzgl. des Aufhängepunktes, Abstand zwischen Aufhängepunkt und Massenmittelpunkt, und der Erdbeschleunigung ab.
Wenn du jetzt ein Haus, mit "Aufhängepunkt" am Boden auslenkst und dann loslässt, würde es mit einer entsprechenden Schwingungsdauer/Frequenz schwingen, seiner Eigenfrequenz.
Wenn das Auslenken/Schütteln zum Beispiel durch ein Erdbeben gerade mit der Eigenfrequenz erfolgt, wächst die Schwingungsamplitude stark an (wie in Maxi's Bild gezeigt). Je weiter du von dieser Eigenfrequenz weg bist, desto geringer ist die Schwingungsamplitude und damit auch eventuelle Schäden am Gebäude.
Je nach Untergrund und Gefährdung, also wie erdbeben-gefährdet ein Gebiet ist, können bestimmte behördliche Auflagen gemacht werden. Zum Beispiel an die Resonanzfrequenz des Gebäudes, oder an die Anzahl der Stockwerke, die auch mit der Resonanzfrequenz zusammenhängt. Oder bestimmte Massen eingebaut werden, die das Trägheitsmoment des Körpers verändern (Schwingungsdämpfer, -tilger).
Die Eigenfrequenz ist recht leicht zu erklären. Am leichtesten zu verstehen oder verständlich zu machen ist es mit einem Fadenpendel und noch leichter mit einer Schaukel.
Du Setzt dein Kind in eine Schaukel und schaukelst es an. Dabei Schwingt die Schaukel hin und her (Ja ich weiß, eine Schaukel ist keine harmonische Schwingung, es geht nur um das zugrunde liegende Prinzip!)
Jetzt stellt sich die Frage, wie schnell du "Schubsen" musst, damit du genau so oft schubst, dass das Kind weiter angeschaukelt wird und und noch stärker schaukelt? Antwort. Du musst das Kind genau so oft anschubsen wie das Kind selber hin und her schaukelt.
Das hin und her Schaukeln des Kindes kannst du als die "Eigenfrequenz" der Schaukel verstehen und die Resonanzfrequenz ist genau die Frequenz mit der du das Kind anschubst.
Wenn du genau diese Frequenz triffst pendelt sich das schaukeln immer höher das heißt durch dein schubsen schaukelt sich das System immer stärker bis zur Resonanzkatastrophe und das Kind sich völlig überschlägt.
Bei einer wackeligen Brücke kann die Resonanzfrequenz auch zum Einsturz führen:
https://www.youtube.com/watch?v=3mclp9QmCGs
Übertragen wir das auf ein Gebäude. Wenn nun ein Erdbeben entsteht, dann wackelt das Gebäude hin und her. Wenn das beben nun genau mit der selben Frequenz bebt wie das Gebäude hin und her schaukelt, dann wird das schaukeln immer stärker bis es schlussendlich zur Resonanzkatastrophe kommt und das Gebäude einstürzt. Wie kann man das Best möglich verhindern?
In Taipeh, der Hauptstadt von Taiwan steht ein Wolkenkratzer, genannt "Taipei One o" Die Höhe beträgt rund 0,5km und ist ständig Einsturzgefährdet. Die eurasische und die philippinische Kontinentalplatten treffen genau hier in der Nähe aufeinander was regelmäßig zu Erdbeben führt. Außerdem ziehen regelmäßig Taifune über diesen hinweg. Wie kann es sein, dass der Wolkenkratzer dennoch all die Erschütterungen überlebt?
Genau dazu haben sich Ingenieure etwas geniales überlegt sie haben im 90. Stockwerk des Gebäudes eine 700 Tonnen schwere Stahlkugel mit einem Durchmesser von 5,5m, an armdicke Stahlseile aufgehängt. Es handelt sich um das größte Pendel der Welt.
Sobald der Turm nun in Schwingung gerät schwingt das Pendel genau gegensinnig zum Turm was die Schwingungen größtenteils kompensiert und so den Turm stabil hält.
Woher wussten Die Ingenieure wie lang die Seile sein mussten und wie schwer die Kugel sein muss? Dazu haben sie Langrange Funktion verwendet. Mit der Lagrange Funktion können sämtliche Newtonschen Bewegungsgleichungen hergeleitet werden, das ist aber sehr theoretisch und für die Resonanzfrequenz alleine gar nicht notwendig.
Die Eigenfrequenz ist die Frequenz mit der ein Körper schwingt. Resonanz ist wenn die ungedämpfte Eigenfrequenz nahe der Anregungsfrequenz liegt und dadurch die Amplitude des angeregten Körpers deutlich größer wird. Man spricht auch von einer ,,Resonanzkatastrophe". Bei einem erdbebensicheren Gebäude sollte die Eigenfrequenz des Gebäudes deutlich unter der Frequenz des Erdbebens liegen, da die Amplitude der Schwingung eines Körpers wenn Omega > Omega0 mit 1/Omega² abnimmt. Omega ist hierbei die Anregungsfrequenz und Omega0 die ungedämpfte Eigenfrequenz.
Im angehängten Bild wird f0 äquivalent zu Omega0 genutzt. Erregerfrequenz wurde von mir als Omega bezeichnet
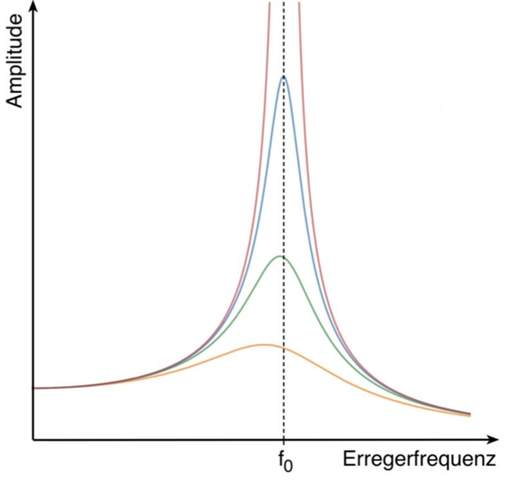
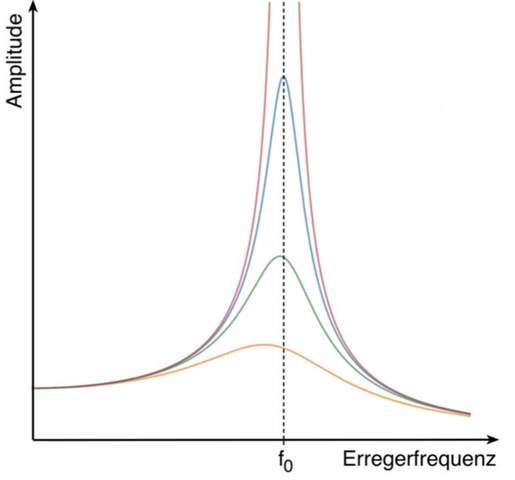
Wird ein schwingfähiges System von außen periodisch, ergo mit einer bestimmten Frequenz,
Energie zugeführt, so führt dieses System erzwungene Schwingungen mit der Erregerfrequenz aus. Bei einmaliger Energiezufuhr schwingt dieses System jedoch frei mit der Eigenfrequenz.
Je mehr Erregerfrequenz und Eigenfrequenz einander angenähert werden, desto größer wird die Schwingungsamplitude. Stimmen Erregerfrequenz und Eigenfrequenz überein, dann ist die maximale Schwingungsamplitude erreicht.
Die Erregerfrequenz heißt in diesen Fall Resonanzfrequenz.
LG H.