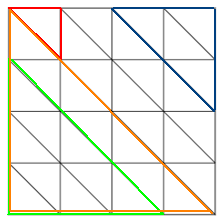
Wie kann ich effizient alle möglichen Dreiecke einer Figur bestimmen?
Ich versuche mich zur Zeit auf ein paar Mathe-Wettbewerbe vorzubereiten und dabei ist mir aufgefallen, dass das Zählen von bestimmten Formen (meistens Dreiecke) die man in einer Figur sehen kann häufig gefragt ist. Hier ein Beispiel mit Dreiecken:
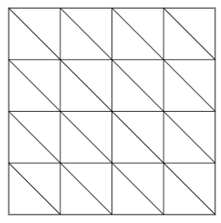
Ich sehe in dieser Figur z.B 60 Dreiecke, nach erneutem Durchzählen, denn beim ersten Mal bin ich auf 58 Dreicke gekommen. Ich frage mich jetzt, ob es hierfür irgendeine Taktik gibt, mit der man solche Aufgaben ganz schnell lösen kann.
2 Antworten
Ich überlege mir zuerst, welche Dreiecke bis auf Verschiebung möglich sind und zähle nacheinander. Hier gibt es von einer Kongruenzklasse immer noch die gespiegelte / gedrehte Variante, sodass einmal der rechte Winkel links unten und das andere mal rechts oben ist. Man kann sich also die beiden getrennt anschauen oder hier nur einmal und dann mal zwei nehmen.
Um zu zählen, wie viele Dreiecke bis auf Verschiebung es gibt, konzentriere ich mich auf einen Punkt, hier z.B. der linke obere Punkt und schaue wie weit unten er maximal sein kann, dass es ein Dreieck gibt und wie weit rechts. Und dann gehe ich durch und zähle die entsprechenden Ecken. In dem Fall haben wir 2⋅(16+9+4+1) = 60 Dreiecke.
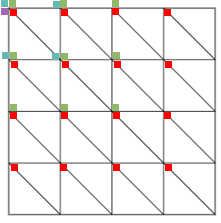
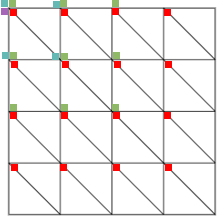
Tolle Idee! Dein Lösungsweg gefällt mir sehr! Werde ich mir auf jeden Fall merken!
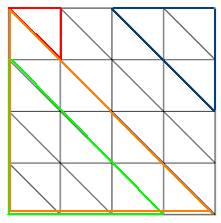
rote Dreiecke: 2 x 4 x 4 = 32
blaue Dreiecke: 2 x 3 x 3 = 18
grüne Dreiecke: 2 x 2 x 2 = 8
orangene Dreiecke: 2 x 1 x 1 = 2
Erkenne das System