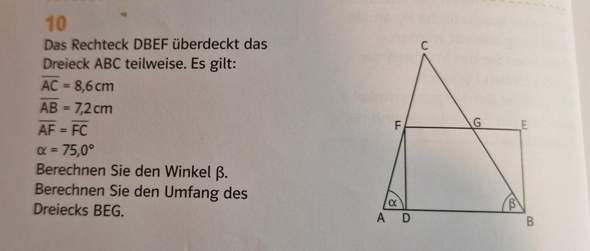
Wie berechne ich den Winkel Beta und den Umfang des Dreiecks BEG?
Ich lerne für die Trigonometrie-Prüfung, die ich schreiben werde, und komme bei dieser Übung nicht weiter.
2 Antworten
Hallo,
da AF=FC, ist AF halb so lang wie AC und AC ist gegeben.
Da auch alpha gegeben ist und der Winkel ADF ein rechter Winkel ist, läßt sich DF=BE über den Sinus, AD über den Kosinus berechnen.
Nach dem zweiten Strahlensatz ist FG halb so lang wie AB.
DB=FE ist gleich AB minus AD.
GE ist gleich FE minus FG.
Aus GE und BE läßt sich über den Satz des Pythagoras BG berechnen; damit halt man alle drei Seiten des Dreiecks BEG und damit auch seinen Umfang.
Da eine Senkrechte von G auf AB genauso lang wie BE ist und BG nun auch bekannt, läßt sich beta aus dem Arkussinus von BE durch BG berechnen.
Herzliche Grüße,
Willy
Seite BC mittels Kosinussatz, Winkel β mittels Sinussatz, ...