Thermoskanne, wieviel K/h verliert sie ungefaehr?
Hallo!
Wenn ich eine Thermoskanne habe, in der 90 Grad heisses Wasser ist, und die Aussentemperatur ist Zimmertemperatur, wieviel Kelvin pro Stunde verliert die ungefaehr? (Richtwert) - diese Information ist aeusserst schwer zu finden und berechnen kann ich sie nicht...
Danke!
5 Antworten
Ich nehme als Rechenbeispiel mal die Werte aus der Antwort von jepet:
T0 = 90Grad, T(3)=50Grad, Ta=20Grad (Zimmertemperatur). Dann gilt:
50=20+(e^3)^(k/mc) * (90-20)
=> 30/70 = (e^3)^(k/mc)
=> k/mc = ln(30/70)/3 = -0,28.
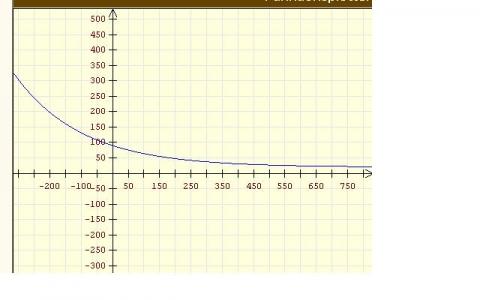
Damit ergibt sich T(t) = 20 + e^(-0,28 * t) * 70.
In der Zeichnung ist der Temperaturverlauf über der Zeit aufgetragen, (Zeit in Minuten).
Also Berechnung ist nicht. Ein Erfahrungswert: Wenn wir 90° heißes wasser einfüllen, hat es nach 3 Stunden noch etwa 50°. Aber es gibt verschiedene Kannen.
Also, Kelvin ist dochg genau wie grad, nur dass nicht der Gefrierwert sondern der absolute Nullpunkt aélso -272 der Nullwert ist. Sagen wir in deinem Zimmer sind 20 Grad, dann hast du 292 Kelvin in deinem Zimmer.
Das musst du selbst ausrechnen. Ohne die genauen Werte kann ich das leider nicht. Du benötigst z.B die Wärmeleitkapazität des Materials etc.
Hallo!
Naja, ich dachte, es gäbe da Richtwerte für eine "durchschnittliche Thermoskanne". Ich bin kein Profi-Physiker und deshalb würde ich das nicht hinbekommen, nichtmal wenn ich die genaue Form/Maße/Materialien der Kanne hätte.
Kannst Du nicht einen GROBEN Richtwert nennen? :)
Da müsste ich in der Literatur nachschauen. Aus dem Stehgreif wüsste ich das leider nicht. Aber lks72 hat ja schon eine tolle Antwort gegeben. Kannst du damit etwas anfangen?
Die Angabe einer Temperaturdifferenz pro Stunde bringt dich nicht weiter, denn der Wärmeverlust der Kaffekanne hängt von der Temperaturdifferenz zwischen innen und außen ab. Bei 40 Grad Unterschied verliert die Kanne doppelt so viel Energie pro Sekunde wie bei 20 Grad Unterschied. Die Geschwindigkeit des Temperaturrückgangs nimmt also immer mehr ab.
Wie fit bist du in Mathe?
Der Energieverlust dE ist proportionale zur Temperaturdifferenz (T-Ta), also etwa
dE = k * (T-Ta). Nun ist dE = m * c * dT, also
m * c * dT = k * (T-Ta), also
dT/(T-Ta) = k / ( m * c).
Integrieren beider Seiten bringt
ln(T(t)) = k/mc * t + konstante, daher
T(t) = e^(k/mc * t) * e^konstante.
Ist T0 die Anfangstemperatur, dann hast du
T(t) = e^(k/mc * t) * T0.
Dies ist eine exponentiell fallende Funktion (k ist ja negativ!).
Miss dir die Werte für k aus, dann kannst du rechnen.
Ich muss mich natürlich korrigieren, ab der 6. letzten Zeile habe ich einfach das Ta vergessen, es muss also weiter heißen:
ln(T-Ta) = k/mc * t + konstante, und weiter dann
ln(T-Ta) = k/mc * t + ln(T0-Ta).
T-Ta = e^(k/mc * t) * (T0-Ta).
T(t) = Ta + e^(k/mc * t) * (T0-Ta).
Was ist das denn bitte? Völlig am Thema vorbei.