Theoretische Informatik Äquivalenzklassen?
Nach Satz von Myhill-Nerode
(a) L = {a(b^k)c | k ∈ No} No sind die natürlichen Zahlen mit 0
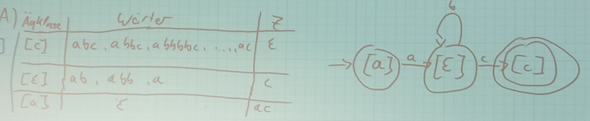
Warum gibt es hier genau 3 Äquivalenzklassen? Der Suffix Z ist einmal epsi, c und ac.
Soweit ok.
Warum schaut man sich nicht als Suffix z. B. bc, oder bbc, oder bbbc an?
1 Antwort
offensichtlich ist a(b^k)c regulär... den endlichen Automaten hast du ja schon...
du suchst also zu Übungszwecken die zugehörige Nerode-Relation...
also nehmen wir mal Suffix „bc“: das passt an alles, was schon mit „a“ anfängt, aber kein „c“ enthält und auch kein weiteres „a“ enthält... und das ist widerrum bereits in Klasse [ε] enthalten... stimmt's? also wäre eine Äquivalenzklasse, die das Suffix „(b^n)c“ hat, in Klasse [ε] enthalten...
und Suffixe können nur „ε“ sein (wenn es schon ein Wort der Sprache ist), oder „c“ (wenn noch ein „c“ fehlt), oder eben „ac“ (wenn noch nix da ist)... eine vierte Möglichkeit zur Ergänzung gibt es nicht, wenn ein Wort der Sprache rauskommen soll...
sag ich mal so... ich mach das zum ersten Mal...
kann ich bitte das goldene Sternchen haben? ich sammel die nämlich... 😋
Du bist der einzige der geantwortet hat bisher. Schau ma ma, was noch kommt. Aber verdient hast es dir eigentlich.
Nächste Frage ist drinnen. Bitte weiterhelfen.
Ich hab noch so ne Aufgabe stell ich gleich mal ein