Heronverfahren Java Quadratwurzel von 2?
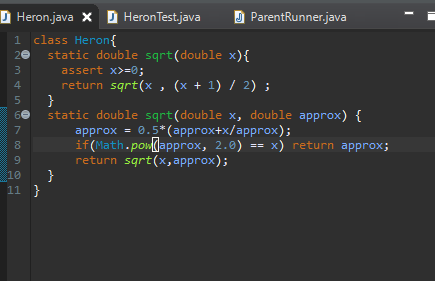
Guten Abend, derzeit habe ich in meinem Informatik Studium die Aufgabe, eine Methode zu schreiben, die die Quadratwurzel einer beliebigen Zahl ausrechnet. Ich bin soweit, dass viele Eingaben funktionieren. Ein Problem habe ich bei der Zahl "2". Und zwar habe ich das Heronverfahren rekursiv geschrieben und als Abbruchbedingung ein if, dass die variable approx mit der eingegebenen Zahl vergleicht. Problem jetzt, die Quadratwurzel aus 2 hat unendlich viele Nachkommastellen und da so die Abbruchbedingung nicht erfüllt wird endet es in einer Endlosschleife.(alles davon auch im Bild zu sehen)
Habe auch schon mit Math.round probiert aber da fängt er an zu früh aus der Schleife zu springen und das Ergebnis stimmt dann nicht mit der Lösung überein. Habe ihr eventuell Lösungsvorschläge ?:D
Vielen Dank schonmal :')
2 Antworten
Es handelt sich doch um ein Annäherungsverfahren. Das heißt, mit jeder Iteration wird dein Ergebnis genauer, aber ja, du kannst dabei auch gegen einen unendlichen Wert konvergieren.
a) Du legst einen Präzisionswert fest, wie viele Annäherungsschritte es maximal geben soll. Wenn diese durchlaufen wurden, wird das Ergebnis so wie es ist genommen.
b) Du definierst eine Zieldifferenz. Erst wenn diese eingehalten wird, bricht die Rekursion ab. Dabei müsstest du aber vorsichtig sein und wieder etwas probieren, andernfalls löst sich dein Problem nicht.
Du gibst alle notwendigen Werte als Parameter mit. Da wäre also einmal ein Parameter, der dir die aktuelle Anzahl an Durchläufen (Rekursionstiefe) verrät und einen Parameter, der die maximale Rekursionstiefe bestimmt. Je Schritt wird dann geprüft, ob der erste Parameter den selben Wert wie der zweite Parameter erreicht hat.
Pseudocode:
repeat(iteration, maxIteration):
if (iteration == maxIteration):
return
repeat(iteration + 1, maxIteration)
# call:
repeat(0, 6)
Das Beispiel kannst du für deinen Fall adaptieren.
Von Prüfen auf Gleichheit ist bei Fließkommazahlen grundsätzlich abzuraten. Das kann immer schiefgehen. Üblicherweise prüft man, ob die Abweichung kleiner ist als ein vorgegebener Wert ("epsilon").
Daneben oder stattdessen kann man auch eine (maximale) Anzahl von Schleifendurchläufen angeben - dazu ist es aber hilfreich, wenn man am Anfang schon eine Abschätzung machen kann. (Hierzu hilft es zu wissen, dass das Heron-Verfahren das Newton-Verfahren für die Quadratwurzel ist)
Alternativ prüft man, ob man auf einen periodischen Umlauf kommt - wenn das Verfahren in der Theorie konvergiert und in der Praxis nicht divergiert, stößt man immer irgendwann auf eine Periode.
Danke für die Hilfe, also das man auf die Schleifendurchgänge prüft hatte ich auch im Kopf aber ich wollte es rekursiv schreiben. Und wie genau würde ich auf epsilon prüfen. Ich kenne epsilon nur beim Grenzwert/ Limes aber wüsste jetzt nicht wie ich das einbauen könnte..
Frage hat sich erledigt, habe es mit Epsilon hinbekommen. Danke für den Tipp !
Danke für die Hilfe, also beim Heronverfahren ändern sich die ersten 5 Nachkommastellen nach 6 Durchgängen ja nicht mehr sind also genau. So wie ich das verstanden habe. Wie genau würde ich dass dann machen. Ich könnte zwar eine Klassenvariable machen und die prüfen aber ich möchte das alles in der Methode schreiben.