Effektivwert, Gleichrichtwert etc. eines gemischten Signals?
Hallo an Alle,
Gegeben ist folgende Aufgabe:
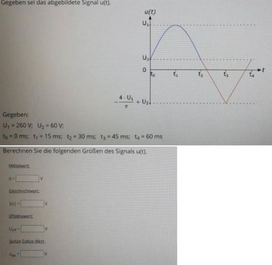
( Entschuldigung für die schlechte Qualität)
Gesucht sind hier:
Mittelwert
Gleichrichtwert
Effektivwert
Spitze-Spitze-Wert
Mein Problem fängt bei der Berechnung der Amplitude des Dreieckssignals an. Da das Signal um U2 schwingt, würde ich sagen û_Dreieck wäre (-4*U1/pi)+U2.
û_Sin ist hier ja U1-U2.
Der Spitze-Spitze-Wert wäre dann die Addition von û_Sinus und û_Dreieck?
Der Effektivwert ist mir klar. Auch das dieser mit dem Gleichanteil Betragsaddiert werden muss.
Für den Mittelwert würde ich rechnen = 1/T * ( [ u_Sin]t0->t2 + [u_Dreieck]t2->t4 )
Der Gleichrichtwert ist für mich noch ein großes Fragezeichen. Muss ich den Gleichrichtwert für das Sinussignal bis t2, und den Gleichrichtwert für das Dreieckssignal einfach addieren?
Den Gleichrichtwert würde ich berechnen indem ich ihn nur für eine viertel Periode des dreieckssignal berechne, und diesen mit dem Faktor 2 multipliziere.
Vielleicht findest sich jemand, der mir helfen kann. Leider habe ich nirgends eine Hilfe gefunden.
Mfg
Ich ergänze nochmals die Aufgabe. Es ist echt schwer zu erkennen:
U1=260V ; U2= 60V; "U3"= (-4*U1/pi)+U2
t0 bis t4 = 0; 15; 30; 45; 60
Leider habe ich nur das Bild zur Verfügung.
Der 2. Teils des Bild wird ersetzt durch die gesuchten Werte die ich beschrieben habe.
Die Sinuskurve fängt bei U1 (t0) an, steigt bis U2(t1) und läuft wieder zurück zu U1(t2).Dann setzt das Dreiecksignal bei U1 und t2 ein. Dieser Verläuft zu (-4*U1/pi)+U2 (t3) und wieder zurück zu U1(t4)
Es ist also ein halbes Sinus-Signal mit einem folgenden halben Dreieckssignal.
Ich kann absolut nichts erkennen und deine Beschreibung ersetzt das Bild nicht. Nochmal mit besserer Auflösung einscannen vielleicht?
Ich habe den Kurvenverlauf nochmal schriftlich ergänzt. Ansonsten könnte ich ihn auch zeichnen und ergänzen. Vielen Dank für dein Interesse :)
1 Antwort
Der Mittelwert ist der Flächeninhalt der Sinushalbwelle + der Flächeninhalt des Dreiecks, geteilt durch die Periodendauer. Sprich das Integral der Sinushalbwelle von t0 bis t2 und des Dreiecks von t2 bis t4. Beachte aber, dass die Spannung hier einen Offset hat, nämlich um +U2.
Für den Gleichrichtwert klappst du gedanklich das Dreieck nach oben um. Mathematisch ist es wie die Rechnung zum Mittelwert, nur dass du hier die Beträge addierst, damit kein negatives Vorzeichen vorkommt.
Der Effektivwert ist der effektive Mittelwert. Auch hier nimmst du die erste Rechnung, allerdings integrierst du quadratisch und ziehst am Ende die Wurzel daraus.
Der Spitze-Spitze-Wert ist, wie der Name sagt, der Abstand zwischen dem höchsten und tiefsten Punkt (Wellenberg beim Sinus und Spitze beim Dreieck).