Doppelspalt - Wellenlänge berechnen?
Ein Doppelspalt mit dem Mittenabstand von 0.8mm wird mit einfarbigem Licht von einer weit entfernten Punktquelle beleuchtet. Auf einem vom Doppelspalt 50 cm entfernten Schirm ein Interferenzmuster.
a) Der Abstand zwischen zwei benachbarten dunklen Interferenzstreifen beträgt 0.304 mm. Berechnen Sie die Wellenlänge des Lichts.
Antwort: λ=(Abstand zweier Maxima/Minima · Mittenabstand)/(Abstand zum Schirm)
also λ=(0.304mm· 0.8mm)/500mm=464.4 Nanometer
b) Schätzen Sie den Spaltabstand ab, bei dem das 1. Maximum vom zentralen Maximum 2 mm entfernt wäre. Begründen Sie ihr ergebnis rechnerisch.
Wie macht man das rechnerisch? Pythagoras?
1 Antwort
Hallo Frage1213,
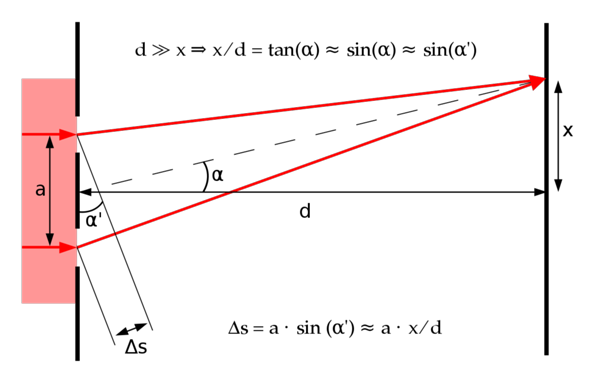
wie die Abstände der Interferenzstreifen mit der Wellenlänge zusammenhängen, ist ganz gut im entsprechenden Wikipedia- Artikel dargestellt, dem ich auch folgendes Bild entnommen habe:
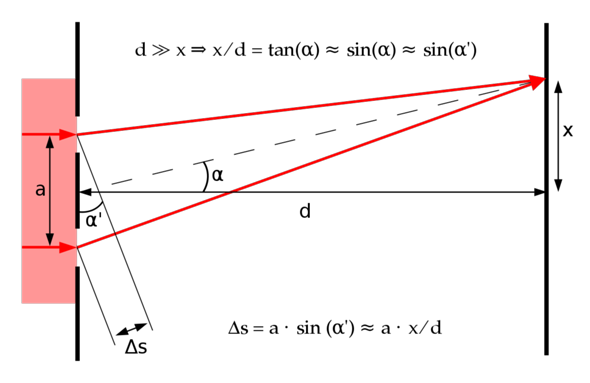
Dabei ist a der in a) erwähnte Abstand zwischen den Mitten der beiden Spalte, und das von Dir erwähnte Ergebnis ergibt sich daraus, dass der Gangunterschied Δs jeweils gleich λ sein soll:
(1) λ = Δs = a∙x⁄d
Dies soll bei b) ebenfalls so sein. Dadas Hauptmaximum und das 1. Maximum ebenfalls benachbart sind, musst Du hier (1) nach a umstellen (λ wird gleich sein):
(2) a = λ∙d⁄x
Aus der Formel wird auch ersichtlich: Je enger die Spalte zusammen sind, desto größer wird der Abstand zwischen zwei benachbarten Maxima bzw. Minima sein.