Elektrischer Stromkreis?
Wie groß ist der Strom im Punkt B in der gezeigten Schaltung, in welche die Widerstände 0,15 kΩ, 50 Ω, und 200 Ω eingebaut sind?
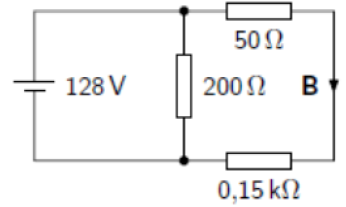
Ich habe mit U = R * I gerechnet und für den Widerstand 200 Ohm genommen. Mein Ansatz hier ist gewesen, dass an dem Knotenpunkt (Wo die Abzweigung zur Parallelschaltung entsteht) der Strom sich aufgrund des Kirchhoffschen Gesetz aufteilt. Folglich ist die Stromstärke im Widerstand identisch zu dem, der sich in an Punkt B befindet? Also ich komme auf das richtige Ergebnis (640 mA) aber ganz verstanden habe ich noch nicht, weshalb ich 200 Ohm benutzen darf bzw. sogar muss.
5 Antworten
Ich würde den Ersatz R berechnen und dan damit durch URI auf den gesamt Strom, weil in beiden parallelen der R gleich groß ist kann man den gesamt A durch 2 teilen und hat somit den Teil A von Punkt B
Nein die 50 und die 150 zusammen in Reihe und dan noch die 200 parallel dazu das fu den gesamt Strom bekommst
Aber wir wollen doch nur an Punkt B die Stromstärke ermitteln. Soweit ich weiss ist die Stromstärke in Parallelschaltungen nicht überall gleich...
Ja stimmt, du brauchst nur die Hälfte von deiner hauptspannung 182 V also 64 V und 200 ohm in deinem parallelen Strang, daraus kannst du dan den Strom in diesem Strang berechnen der auch gleich Groß ist wie der Strom in deinem Strang A, weshalb man es auch über die gesamten Daten hätte rechnen können
Die Lösung der Aufgabe ist 650 mA ich weiss nicht ob ich auf das Ergebnis mit deinem Rechenweg komme
der 200 Ohm Widerstand ist nur eingebaut, um dich zu verwirren. Den kannst du also völlig ignorieren.
Übrig bleibt eine Reihenschaltung zweier Widerstände.
Richtig, die haben einen Gesamtwert von 200 Ohm.
Ist es nicht gleichgültig wo man den Strom messen würde?
In einem Gartenschlauch fließt hinten ja auch so viel Wasser raus, wie vorn rein.
Den Schlauch kann man auch an beliebigen Stellen auftrennen und dort messen, über all gleich. Wie sollte es auch anders sein.
Ahhh ich verstehe, dass stimmt der Strom geht nicht verloren, wird nur an einigen Stellen aufgrund des Widerstandes ,,gedrosselt'' und fließt folglich nicht so schnell. Aber prinzipiell ist der Strom denn ich an Punkt B messe überall gleich in der Reihenschaltung. Deswegen kann ich die Parallelschaltung außer acht lassen, richtig? Danke für deine Super Erklärung habe ich direkt auf anhieb verstanden <3
alles Richtig!
nur den Satz
... der Strom ...wird nur an einigen Stellen aufgrund des Widerstandes ,,gedrosselt''
würde ich so nicht schreiben.
Wenn man das räumlich betrachtet, sind die Widerstände hier an unterschiedlichen (an einigen) Stellen vorhanden. Zeitlich gesehen, fließt an anderen Stellen aber nicht mehr Strom, es fließt überall in dem Kreis
(Draht,--> 50 Ohm Widerstand -> Draht -> 150 Ohm Widerstand ->Draht) der gleiche Strom. Ab Verbindungspunkt 200 Ohm-Widerstand bis zur Spannungsquelle kommt dann natürlich auch noch der Strom hinzu, der nur durch den 200 Ohm Widerstand fließt.
Ahhh das stimmt, dass hast du sehr schön erklärt. Da kommen sogar Holzköpfe wie ich mit ;D
nee, Holz leitet Strom fast nicht und kann schon gar nicht verstehen, wie das mit Strom so ist.
Ich kann mich noch recht gut an meine Schulzeit daran erinnern und an die Probleme, die ich mal mit solchen Fragen hatte.
Es ist also nicht zu spät. Aus mir ist auch noch was geworden.
Wieso nimmt man die ursprüngliche Spannung von 128 V und wieso wird sie nicht „gefällt“
Die Quelle ist als ideale Spannungsquelle zu betrachten, sie hat einen Innenwiderstand von Null Ohm. Damit bleibt sie konstant bei ,(hier) 128V
Das Ergebnis ist richtig, da der 200 Ohm-Widerstand auf den Stromfluß bei B keinen Einfluß hat und somit nur durch die Widerstände 0.15 kOhm und 50 Ohm ( ebenfalls 200 Ohm ) beeinflußt wird. Der Gesamtstrom an der Batterie beträgt aber 1.28 A, weil zwei 200- Ohm-Widerstände parallelgeschaltet sind, aber danach war ja nicht gefragt.
Der Strom teilt sich an der Verzweigung auf.
Der 200Ohm Widerstand spielt im Prinzip keine Rolle, nur die beiden anderen Widerstände.
Wieso? Weil der Strom nicht durch ihn fließt? Aber durch 150 Ohm zu teilen ist ja auch falsch....
Weil der Strom nicht durch ihn fließt?
Genau!
Aber durch 150 Ohm zu teilen ist ja auch falsch....
Ja, weil dort 2 Widerstände sind!
Ich bin etwas verwirrt, weil die Stromstärke an Punkt B ermittelt werden soll. Der Widerstand mit 150 Ohm ist aber vor dem Punkt. Also ist der Strom noch nicht durch ihn geflossen. Weshalb inkludiere ich den Widerstand dann in meine Rechnung?
Der Strom fließt doch durch beide Widerstände!
Also 150 +50 !
Wo soll er denn hin???
Seit wann fließt ein Strom in zwei Richtungen?!
Außerdem ist er an Punkt B (siehe Abbildung) eben noch nicht durch beide Widerstände geflossen oder wie meinst du das?
Tut er auch nicht! Trotzdem fließt der gleiche Strom durch beide Widerstände.
Egal! Durch beide Widerstände fließt der gleiche Strom. Vorher und hinterher auch!
Wo soll er denn sonst hin???
Es MUSS der gleiche Strom sein!
aber das wäre der Storm, der Strom der sich am ersten Knotenpunkt aufteilt richtig? Deswegen rechne ich den Strom für 200 Ohm aus (Reihenschaltung). Ich glaube ich habs jetzt oder auch nicht :D
Ja das ist korrekt mit 200 Ohm zu rechnen... Und auch das Ergebnis ist richtig...
die Spannung 128V steht sowohl an dem 200 Ohm Widerstand an, wie auch an der Reihenschaltung des 50 Ohm und 150 Ohm Widerstand.. Somit gilt für jeden Strang I_strang = U0 / R_strang...
Ich versteh aber nicht weshalb der 150er Widerstand miteinbezogen werden kann/muss --> Der Strom fließt ja nach Punkt B durch den Widerstand. Oder versteh ich was falsch?
Ersatz R wäre Punkt B also 128 V / 150 Ohm und dann durch 2 teilen?