Wie programmiere ich den Bubblesort in Java (Processing)?

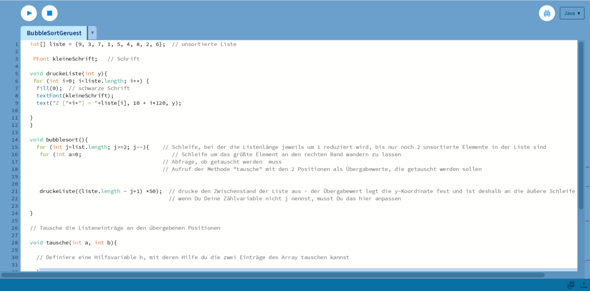
Zurzeit nehmen wir das Thema "Sortieralgorithmen" in der Schule durch und wir sollten als Project den Bubblesort in Processing programmieren. Dafür haben wir von unserer Lehrerin eine Vorlage bekommen, aber ich verstehe kaum etwas. Großteil der Elemente im Code haben wir im Unterricht noch nicht durchgenommen, wodurch für mich noch sehr viele Fragen in der Luft stehen. Als Zusammenfassung was wir schon im Unterricht gemacht haben: Methoden zum Zeichnen, Syntax einer Zahlenschleife, Deklarieren und Initialisieren, Setup, Verschiedene Arten von Methoden (mit Rückgabewert/Übergabenparameter oder ohne Rückgabewert) und Arrays. Dazu noch habe ich die Hilfe if (a>b){ und das Drucken vom Text in ein definiertes Fenster. Ich hab bei den ersten zwei Anweisungen schon etwas reingeschrieben, aber ich bin mir unsicher, ob ich es richtig mache oder in die komplett falsche Richtung gehe. Über eine Lösung oder weitere Hilfestellung würde ich mich deswegen sehr freuen.

Bild zum Beitrag

1 Antwort

regex9

Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer

Java, Programmiersprache, Programmieren & Softwareentwicklung

24.04.2023, 22:11

(...) aber ich verstehe kaum etwas.

Entweder du formulierst konkrete Fragen dazu, oder du musst selbst recherchieren. Processing hat eine Referenz, in der du zu jedem Schlüsselwort auch einen erklärenden Artikel findest.

Geh zeilenweise durch die bestehenden Zeilen und statte sie mit Kommentaren aus oder schreibe parallel stichpunktartig auf, was du deuten kannst. Es ist im Grunde so, wie bei einem Text in Fremdsprache, den du übersetzen möchtest. Teile auf, übersetze und füge es dann wieder zusammen, um dir ein Gesamtbild verschaffen zu können.

(...) aber ich bin mir unsicher, ob ich es richtig mache oder in die komplett falsche Richtung gehe. (...)

Finde erst einmal eine Lösung völlig fernab vom Code. Im ersten Schritt musst du erst einmal erfassen, wie der Bubblesort überhaupt funktioniert, danach kannst du die Teilschritte ermitteln.

Zu Ersterem: Beim Bubblesort geht es darum, das stets größte Element aus einer Menge zu finden und an deren Ende zu sortieren. Dafür geht man über alle Elemente der Menge und greift sich immer zwei aufeinanderfolgende Elemente heraus, die miteinander verglichen werden. Wenn das erste Element größer ist als das zweite Element, werden ihre Positionen vertauscht. So sollte spätestens nach einem kompletten Durchlauf durch die Menge das größte Element am Ende stehen. Es kann als korrekt sortiert betrachtet werden.

Diesen Sortiervorgang kann man nun wiederholen, allerdings betrachtet man nur noch die unsortierten Elemente. Nach mehreren Sortiervorgängen wird es irgendwann nur noch ein unsortiertes Element geben. Da sich dessen Position nicht mehr ändert, ist das Programm an diesem Zeitpunkt fertig.

Das einmal an einem konkreten Beispiel demonstriert:

Durchlauf 1 mit der zu sortierenden Menge: [ 3, 2, 5, 1 ]
  3 > 2 => Tausch
  [ 2, 3, 5, 1 ]
  3 < 5 => kein Tausch
  [ 2, 3, 5, 1 ]
  5 > 1 => Tausch
  [ 2, 3, 1, 5 ]

Durchlauf 2 mit der zu sortierenden Menge [ 2, 3, 1 ] (die 5 wird von nun an ignoriert)
  2 < 3 => kein Tausch
  [ 2, 3, 1 ]
  3 > 1 => Tausch
  [ 2, 1, 3 ]

Durchlauf 3 mit der zu sortierenden Menge [ 2, 1 ] (3 und 5 werden von nun an ignoriert)
  [ 2, 1 ]
  2 > 1 => Tausch
  [ 1, 2 ]

Durchlauf 4 mit der zu sortierenden Menge [ 1 ] (2, 3 und 5 werden von nun an ignoriert)
  Da es nur noch ein Element gibt, kann man schlussfolgern, dass die Liste nun sortiert sein muss.

Zu Zweiterem: Versuche den Ablauf erst einmal mit einem Struktogramm oder einen Programmablaufplan nachzubilden. Verwende nur einfachste Bausteine (Variablen erstellen/lesen, Abfragen, Wiederholungen). Was komplexer ist, muss aufgebrochen werden. Für das Tauschen zweier Elemente beispielsweise eignet sich ein eigener Plan. Deine Lehrerin hat dir offensichtlich in der Vorlage auch bereits angedeutet, dass du diesen Prozess separat (als Funktion) lösen sollst.

Erst wenn du einen Algorithmus mit einfachen Teilschritten geformt hast und ihn an einem beliebigen Beispiel (einer beliebigen Liste an Zahlen) erfoglreich testen konntest, folgt der Teil, bei dem du die Teilschritte in konkreten Quellcode übersetzt. Das sollte nur noch Fleißarbeit sein. Mehr als die Themen, die ihr im Unterricht bereits behandelt habt, brauchst du nicht.

Hallo! Ich schreibe morgen eine Informatik Klausur über Sortieralgorithmen. Meine Frage ist erstmal was versteht man genau unter Effizienz und wann die folgenden Algorithmen besonders effizient bzw. ineffizient arbeiten: BubbleSort, InsertionSort, SelectionSort, MergeSort und QuickSort. Danke im voraus

...zur Frage

Java Arrays?

Wir haben die Aufgabe bekommen dieses Programm umzuschreiben, sodass keine Schleifen vorkommen nur if, if else und else if. Sprich er soll sortieren aber nur mit den if abfragen.

Wir sollen Aufgabe 1 a) machen wie es oben in dem Bild geschrieben ist

public class Main
{
    public static void main(String[] args)
    {
        //Array deklarieren und initialisieren
        int[] array=new int[]{3,1,2};

        //Array sortieren
        for (int j=0; j<array.length-1;j++)
        {

            for (int i=0;i<array.length-1-j;i++)
            {

                //falls linkes Element größer > tauscht mit rechts
                if(array[i]>array[i+1])
                {
                    //tauschen
                    int memory=array[i];
                    array[i]=array[i+1];
                    array[i+1]=memory;
                }
            }
        }

        //Array ausgeben
        System.out.println("Anzahl der Schritte: ");


        //zählt die einzelnen zahlen bis er durch ist
        for(int i=0;i < array.length;i++)
        {
            System.out.print(array[i]+" ");
        }
    }

...zur Frage

BubbleSort Code Verständnisfrage?

BubbleSort in Java:

Wieso rechnet man in der zweiten for-Schleife (liste.lenght - k) ?

Sobald es der 4. Durchgang ist, ist doch b < (liste.lenght - k) nicht mehr erfüllt oder, weil b dann 3 ist und (liste.lenght - k) ebenfalls 3.

...zur Frage

Wie kann ich JavaScript-Code in Processing-Code umschreiben?

Hallo,

also ist es möglich, einen Java-Code in einen Processing-Code umzuschreiben oder besser gesagt, könnte jemand helfen? Ich bin noch sehr am Anfang, habe aber einen Code gefunden, der mir sehr gut gefällt und mit dem ich gerne ein bisschen herumprobieren würde. Nur funktioniert er eben in Processing nicht und mit Java kenne ich mich noch weniger aus, darum würde ich ihn gerne umschreiben.

So sieht das Ganze aus:

let shapes = [];
let colors = ["#ffc857", "#e9724c", "#c5283d", "#481d24", "#255f85", "#a5bccc"];

function setup() {
  createCanvas(1000, 800);
  rectMode(CENTER);
  translate(width / 2, height / 2);
  scale(1.4);
  rotate(random(PI));
  translate(-width / 2, -height / 2);
  background(random(colors));
  let seg = int(random(25, 45));
  let w = width / seg;

  for (let i = 0; i < seg; i++) {
    for (let j = 0; j < seg; j++) {
      let x = i * w;
      let y = j * w;

      if ((i + j) % 2 == 0) {
        shapes.push(createVector(x + w / 2, y + w / 2, w * 2.01));
      }
    }
  }

  shuffle(shapes, true)
  noStroke();

  for (let s of shapes) {
    let rnd = int(random(4));
    shuffle(colors, true);
    push();
    translate(s.x, s.y);
    fill(random(colors));

    if (rnd == 0)
      circle(0, 0, s.z);
    else if (rnd == 1)
      square(0, 0, s.z);
    else if (rnd == 2) {
      let n = int(random(1, 5));
      
      for (let i = 0; i < n; i++) {
        let ss = map(i, 0, n, s.z, 0);
        fill(colors[i]);
        circle(0, 0, ss);
      }
    }
    else if (rnd == 3) {
      let n = int(random(1, 10));

      for (let i = 0; i < n; i++) {
        let ss = map(i, 0, n, s.z, 0);
        fill(colors[i % colors.length]);
        square(0, 0, ss);
      }
    }

    pop();
  }
}

function draw() {
}

...zur Frage

java array umdrehen?

Auf meiner IT Schule habe ich diese aufgabe bekommen aber komme nicht wirklich weiter. Kann mir jemand vielleicht helfen?

...zur Frage

wie kann ich durch einen baum iterieren Java?

package ListenInJava.Baume;


public class TreeNode {
    int data;
    TreeNode left;
    TreeNode right;


    TreeNode(int data){
        this.data = data;
        this.left = null;
        this.left = null;
    }
}





package ListenInJava.Baume;


public class Tree {
    TreeNode root;


    Tree (){
        root = null;
    }


    public void add(int data){
        TreeNode t1 = new TreeNode(data);
        if(root == null){
            root = t1; 
            return;
        }
        TreeNode help = root;
        while(help != null){
            if(help.data > t1.data){
                
                if(help.left == null){
                    help.left = t1;
                    return;
                }
                help = help.left;
            } else{
                if(help.right == null){
                    help.right = t1;
                    return;
                }
              help = help.right;   
            }
        }
        return;
    }


 
}

ich möchte dann den baum in form von:

root

left right

usw. haben, aber wie genau könnte ich denn durch den baum iterieren mit einer schleife?

...zur Frage

Ist es möglich ein Processing-Programm in eine Android APK zu konvertieren?

Kann man ein Programm der Sprache Processing in eine Android APK umwandeln? Wenn ja bitte erklären wie!

...zur Frage

Processing Java Farben wechselnder Kreis?

Ich habe diesen code:

void setup() {

size(700,700);

frameRate(99999);

float y = 1;

}

void draw() {

noStroke();

ellipse(mouseX,mouseY,50,50);

}

Ich würde gerne noch hinzufügen, das der Kreis flüssig seine Farbe wechselt, im verlauf eines Regenbogens. Wie geht das?

...zur Frage

Wie erstelle ich in Processing Rot13?

Zu erstellen ist ein Processing-Programm, bei dem sich beim Starten ein Eingabefenster öffnet in welches ein Text aus Groß- und Kleinbuchstaben, sowie Kommata und Punkte eingegeben wird. Nach Bestätigung der Eingabe soll dieser Text "ROT13"-verschlüsselt auf der Konsole oder in einem Textfeld ausgegeben werden.

Ich bedanke mich für jede Hilfe im voraus schonmal!

...zur Frage

LinkedList in Java sortieren beim Einfügen eines neuen Elements?

Ich habe hier den Code geschrieben, um ein neues Element einzufügen und danach die Liste zu sortieren.

Ich weiss, dass beides (Algorithmus für einfügen & Algorithmus fürs Sortieren) einzeln eigentlich funktionieren sollte. Aber die Kombination davon in einer Methode scheitert. Sieht jemand den Fehler.

Herzlichen Dank im Voraus!

...zur Frage

Fakultät-Rechner in Java programmieren?

Ich habe folgendes Programm:

public class test {
    public static void main(String[] args) {
      System.out.println(fakulteat(5));
    }
    
    public static int fakulteat(int zahl) {
      if (zahl == 1) {
        return 1;
      } else {
        return zahl * fakulteat(zahl - 1);
      }
    }
}

Hier wird jetzt ja die Fakultät berechnet durch diese rekursive Methode.

Mein Problem steckt folgender Zeile:

return zahl * fakulteat(zahl - 1);

Damit gibt man dann so gesagt " 5 * 4! " an die Methode zurück.

Was ich mich aber Frage ist halt, wieso " fakulteat(zahl - 1) " jetzt eine Fakultät darstellt. Der Methode gibt sich selbst damit doch nur einen Wert zurück, woher weiß aber die Methode, dass dann z.B. 4! = 1 * 2 * 3 * 4 gemeint ist?

...zur Frage

Java Arrays Buchstaben als Zahlen ausgeben?

Hi, ich habe eine Aufgabe, bei der ich schon die Aufgabenstellung nicht verstehe, geschweige denn, die Aufgabe selbst.

Aufgabe: (Methode: toDoubleArray)

Modifikatoren: public und static, Rückgabetyp: double-Array , Methodenname: toDoubleArray , Übergabeparameter: String

Schreibe eine Methode, die ein double-Array erzeugt und es mit den einzelnen Zeichen (char) aus dem String befüllt.
Allerdings werden diese Werte vor Zuweisung noch nach double gecastet. Anschließend wird das double-Array zurück gegeben.

Beispiel: Der Aufruf toDoubleArray("Hallo") liefert ein Array, das folgendermaßen befüllt ist: [72.0, 97.0, 108.0, 108.0, 111.0]

Das casten verstehe ich. Ist ja nur eine Typumwandlung von char nach double und geschieht automatisch, weil char in double passt. Hier ein Beispiel:

public static void main(String [] args) {	

		char t = 'a';

		System.out.println(t);
        System.out.println((double) t);
  }
}		

Ausgabe : a
          97.0

> char als Buchstabe und als Zahl

Wie soll ich jetzt den ersten Teil der Aufgabe machen, also die Zeichen (char) aus dem String ins Array bringen????

Wie füge ich die Zeichen in erster Linie ins Array?

...zur Frage

Kann man diesen Array so darstellen?

Hey, Frage in der Klausur: Man soll zwei Arrays deklarieren und eines davon mit Werten initialisieren, die auch gegeben waren. Zunächst soll man die gegeben Werte in den anderen delarierten Array übertragen, aber doppelt. Ich habe es sehr ausführlich gemacht aber es ist ja wichtig, das das richtige Resultat erfolgt. So habe ich es gemacht:

Deklaration des Arrays zahlen und Initialisierung mit den Werten = [ 100, 56, 78, 67, 90 ]

Deklaration des Arrays zahlenA = [ ]

Deklaration einer Zwischenvariablen z

Deklaration der Zwischenvariablen k und Initialisierung mit dem Wert 2 als Ganzzahl

Zuweisung: z = zahlen [ 0 ]

Zuweisung: zahlenA [ 0 ] = z

Zuweisung: z = zahlen [ 1 ]

Zuweisung: zahlenA [ 1 ] = z

Zuweisung: z = zahlen [ 2 ]

Zuweisung: zahlenA [ 2 ] = z

Zuweisung: z = zahlen [ 3 ]

Zuweisung: zahlenA [ 3 ] = z

Zuweisung: z = zahlen [ 4 ]

Zuweisung: zahlenA [ 4 ] = z

Wiederhole für i = 0, i < 5, i = i + 1

Zuweisung: z = zahlenA [ i ]

Ausgabe: zahlenA [ i ] = k * z

...zur Frage

Wie findet ihr diesen Programmier Stil in C?

In der Schule müssen wir in diesem Stil programmieren:

#include <stdio.h>

int main(void)
{
      printf("Hello, World!");
      return 0;
} // end main

Wir findet ihr das?

Ich finde man sollte selbst entscheiden welchen Programmierstil man verwendet, solange der Code lesbar und verständlich ist.

...zur Frage

Was möchtest Du wissen?

Deine Frage stellen