Wie in Java mit PQ-Formel und statischen Methoden rechnen?

Guten Abend miteinander, unzwar habe ich eine Aufgabe die zu lösen ist, wobei ich leider nicht weiter komme. Die PQ-Formel habe ich hingekriegt, was jedoch mit dem "Satz von Vieta" gemeint und wie dieser anzuwenden ist, ist mir unschlüssig.

Aufgabe: Das Problem für die Lösungsberechnung der Gleichung (x^2 −3 · 10^200 x+2 = 0) ist lösbar. (Die Lösungen lauten x1 ≈ 3 · 10200 und x2 ≈ 7 · 10−201, sind also in Java darstellbar.) Wie muss man vorgehen, damit sie in Java berechnet werden? Hilfreich dazu ist der „Satz von Vieta“, insbesondere die Beziehung x1x2 = q der zwei Lösungen zu q.

Das ist was ich bisher dafür hab:

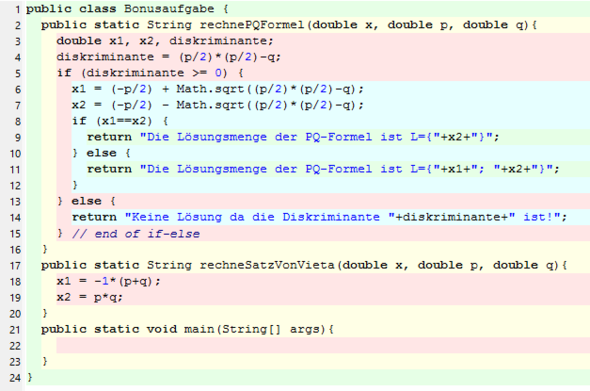
public class Bonusaufgabe { public static String rechnePQFormel(double x, double p, double q){ double x1, x2, diskriminante; diskriminante = (p/2)(p/2)-q; if (diskriminante >= 0) { x1 = (-p/2) + Math.sqrt((p/2)(p/2)-q); x2 = (-p/2) - Math.sqrt((p/2)(p/2)-q); if (x1==x2) { return "Die Lösungsmenge der PQ-Formel ist L={"+x2+"}";
} else { return "Die Lösungsmenge der PQ-Formel ist L={"+x1+"; "+x2+"}"; } } else { return "Keine Lösung da die Diskriminante "+diskriminante+" ist!"; } // end of if-else } public static String rechneSatzVonVieta(double x, double p, double q){ x1 = -1(p+q); x2 = p*q; }
public static void main(String[] args){

} }

PS. weiß leider nicht wie ich mein Programm hier schön einfügen kann, deshalb nochmal als Bild angehangen.

Mein Programm - (Programm, programmieren, Java)

2 Antworten

Eismensch

08.12.2016, 01:46

Du benutzt den Satz von Vieta falsch...

Der Satz sagt aus:

x1 + x2 = -p
x1 * x2 = q

Du benutzt stattdessen:

x1 = -1 + (p+q)
x2 = p * q

Schau dir nochmal den Satz und seinen Beweis an:
https://de.wikipedia.org/wiki/Satzgruppe_von_Vieta

Woher ich das weiß:Berufserfahrung – Java Entwickler

regex9

Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer

Programm, programmieren, Java

08.12.2016, 01:53

Satz von Vieta: http://www.mathebibel.de/satz-von-vieta

Die Wurzelberechnung könntest du noch in eine Variable schreiben, die dann für den positiven und negativen Fall genutzt wird. Dann muss das Programm nicht zweimal das Gleiche (die Wurzel) rechnen.

Ähnliche Beiträge

Java: Wie kann ich den Artikelpreis von einer Artikelliste ändern?

Hallo,

ich habe eine Klasse für die Verwaltung von Artikeln, die eine Bezeichnung, Nummer und einen Preis haben. Ich möchte hier den Preis mit einen gegebenen Prozent ändern.

Die Methode nimmt eine Liste von Artikeln und einen Prozent und ändert den Preis der Artikel. Die Methode habe ich im Kommentar gemacht.

import java.util.Arrays;

public class Article {
  private String bezeichnung; // ArtikelTitel
  private long artikelNr; // Artikelnummer
  private static double preis; // Einzelpreis des Artikels
  private static long AnzahlArtikel;
  private static long nextArtikelNr = 100;

  public Article(String bezeichnung, double preis) {
    this.bezeichnung = bezeichnung;
    Article.preis = preis;
    this.artikelNr = Article.nextArtikelNr++;
    Article.AnzahlArtikel++;
  }

  public Article(String bezeichnung) {
    this(bezeichnung, 0.0);
  }

  public long getartikelNr() {
    return this.artikelNr;
  }

  public String getbezeichnung() {
    return this.bezeichnung;
  }

  public static long getAnzahlArtikel() {
    return Article.AnzahlArtikel;
  }

  public double getPreis() {
    return Article.preis;
  }

  /*
   * public static void changePrices(Article[] articles, double percentage) {
   *
   * if (articles == null || articles.length == 0 || percentage < 0) {
   * return;
   * } else {
   * // Article[] result = new Article[articles.length];
   * double percentageArtikel;
   *
   * for (int i = 0; i < articles.length; i++) {
   * percentageArtikel = artciles[i].getPreis() * percentage;
   * preis += percentageArtikel;
   * }
   * }
   * return;
   *
   * }
   */

  public String toString() {
    return artikelNr + ", " + bezeichnung + ", " + preis;
  }
}

...zum Beitrag

Obejekt orienetiertes Programmieren... wäre das so richtig?

Hallo,

ich weiss das in dem Programmstück das jetzt kommt bestimmt viele fehler sein werden aber ich weiss nur nicht was die fehler sind. Ich arbeite mit Eclipse und es zeigt mir wo die Fehler sind nur weiss ich nicht wie ich diese beheben soll.... Ich hoffe man kann mir helfen. Bin gerade dabei OOP zu lernen und naja... Hier das Programmstück

import java.io.*;

public class Mensakarte { double guthaben; String besitzer; boolean gesperrt;

public Mensakarte(){ guthaben = 0.0; besitzer = "Helene"; gesperrt = true; } public static void main(String args[]) throws IOException {

BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
int choice = 0;
boolean erfolg;

do {
  
  System.out.println();
  System.out.println("Bitte waehlen:");
  System.out.println("(1) Karte aufladen");
  System.out.println("(2) Guthaben anzeigen");
  System.out.println("(3) Kaffee abbuchen");
  System.out.println("(4) Essen abbuchen");
  System.out.println("(5) Verbleibende Kaffees anzeigen");
  System.out.println("(6) Sperre toggeln");
  System.out.println("(0) Ende");
  choice = Integer.parseInt(in.readLine());
  System.out.println();
  
  switch (choice) {
    
    case 1:
    System.out.print("Aufladebetrag? ");
    double betrag = Double.parseDouble(in.readLine());
       aufladen(betrag);
    break;
    
    case 2:
       guthaben();
    break;
    
    case 3:
       kaffe_abbuchen();
    break;
    
    case 4:
    System.out.print("Essenspreis? ");
    double preis = Double.parseDouble(in.readLine());
       essen_abbuchen (guthaben);
    break;
    
    case 5:
      anzahl();
    break;
    
    case 6:
      toggeln();
    break;
    
  }
  
} while (choice!=0);

} public static double aufladen(double plus){ if (plus >=0) {

    guthaben = guthaben + plus;
return guthaben;
}

}
public double guthaben(){
double guthaben=guthaben; return guthaben; }
public boolean kaffe_abbuchen(){ if (guthaben>= 1.20) { guthaben = guthaben - 1.20;

  return true;
}
else {
  return false; 
}

} public boolean essen_abbuchen(double preis){ if (guthaben>=preis) { guthaben = guthaben - preis;

  return true;
}
else {
  return false;
}

} public int anzahl(){ int zahl; zahl = guthaben/1.20;

return guthaben;

}
public boolean toggeln(){ boolean gesperrt;

if (gesperrt=true) {
  return false;
    
  } 
  else {
   return true;   
  }

} }

...zum Beitrag

Java Programm Gleichungssytem 3. Grades/Cramersche Regel?

Hallo, ich habe ein Programm erstellt, dass mithilfe der Cramerschen Regel ein Gleichungssytem 3. Grades löst (siehe unten) Nur kommt bei dem Ergebnis immer x1=0.0, x2=0.0 und x3=0.0 raus, egal was man eingibt. Ich finde den Fehler einfach nicht, kann mir da bitte jemand weiterhelfen?

import java.util.*;
public class gs3 {
    public static void main(String[] args) {
        Scanner ein = new Scanner(System.in);
        System.out.println("Geben Sie den Koeffizienten des Gleichungssystems ein:");
        double[][] m = new double[3][4];
        for (int i = 0; i < 3; i++) {
            System.out.println("Gleichung " + (i + 1) + ":");
            for (int j = 0; j < 3; j++) {
                System.out.println("Koeffizient x" + (j + 1) + ":");
                m[i][j] = ein.nextDouble();
            }
            System.out.println("Rechte Seite: ");
            m[i][3] = ein.nextDouble();
        }
        double determinanteA = calculateDeterminant(m);
        if (determinanteA == 0) {
            System.out.println("Gleichungssystem nicht lösbar.");
        } else {
            double[] ergebnis = new double[3];
            for (int i = 0; i < 3; i++) {
                double[][] modifiedM = modifyM(m, i);
                double determinantModified = calculateDeterminant(modifiedM);
                ergebnis[i] = determinantModified / determinanteA;
            }
            System.out.println("Lösung: x1 = " + ergebnis[0] + ", x2 = " + ergebnis[1] + ", x3 = " +
                ergebnis[2]);
        }
        ein.close();
    }
    private static double calculateDeterminant(double[][] m) {
        double determinante = 0.0;
        determinante = m[0][0] * (m[1][1] * m[2][2] - m[1][2] * m[2][1]) -
            m[0][1] * (m[1][0] * m[2][2] - m[1][2] * m[2][0]) +
            m[0][2] * (m[1][0] * m[2][1] - m[1][1] * m[2][0]);
        return determinante;
    }
    private static double[][] modifyM(double[][] m, int column) {
        double[][] modifiedM = new double[3][3];
        for (int i = 0; i < 3; i++) {
            for (int j = 0, k = 0; j < 3; j++) {
                if (j != column) {
                    modifiedM[i][k++] = m[i][j];
                }
            }
        }
        return modifiedM;
    }
}

...zum Beitrag

Wie löse ich die Javaaufgabe für den goldenen Schnitt?

Hallo liebe Community,

ich habe folgendes Problem: Ich muss eine Javaaufgabe lösen, welche diesen mit konvergenz berechnet. Die vorgegeben Formel lautet wie folgt: g = 1 + 1/g = 1+1/1+1/g = ... Für g wird quasi immer 1+1/g eingesetzt. Mir wird ein Parameter übergeben, welcher bestimmt, wie oft die Abfolge berechnet werden soll. Bei meinem Programm kommt es aber immer wieder zu minimalsten Abweichungen bei der 3.-5. Nachkommastelle und ich weiß nicht wie ich diese Abweichungen beseitigen kann.

Hier noch der bisherige Code:

public class GoldenRatio {

    public static double result;
    public static double result2;
public static double calculate(int n) {
    
    if(n==0){
        return 0;
    }
    for(int i=0;i<=n;i++){
        result = 1+ 1/result;
    }
    return result;
}

}

Ich hoffe ihr könnt mir da irgendwie weiterhelfen.

Viele Grüße Dubsepp

...zum Beitrag

Java Objekte: Wie kann ich meinen Kontostand anzeigen lassen, wenn es 30.00 beträgt und ich 5.00 abhebe?

Ich bin ein absoluter Anfänger in dem Gebiet und habe schon so viel ausprobiert. Nun frage ich euch. Wie muss ich außerdem meinen passenden Konstruktor hier formulieren?

Hier der Code und für bessere Übersichtlichkeit ein Bild:

package konto;

public class konto {
  private double kontostand;

  private String name;

  public void setData(double kontostand, String name) {
    this.kontostand = kontostand;
    this.name = name;
  }

  public double getKontostand(int kontostand) {
    return kontostand;
  }

  public String getName(String name) {
    return name;
  }

  public boolean einzahlen(double betrag, int kontostand) {
    boolean einzahlen = false;

    if (betrag > 0) {
      einzahlen = true;
      kontostand += betrag;
    }

    return einzahlen;
  }

  public boolean abheben(double betrag) {
    boolean abheben = false;

    if (betrag > 0 && kontostand - betrag >= 0) {
      abheben = true;
      kontostand -= betrag;
    }

    return abheben;
  }

  public String alsText(int kontostand, String name) {
    return "kontostand: " + kontostand + "name: " + name;
  }
}

...zum Beitrag

Java: Array Rückwärts ausgeben;?

Ich will praktisch die Ausgabe "1.0, -1.0, -3.0" statt "-3.0, -1.0, 1.0,"

Ich habe es mit Reverse versucht, aber der Fehler ist mir erst aufgefallen, als ich es schon hatte. Eine for-Schleife hat auch nicht geklappt (könnte aber an mangelnden Kenntnissen liegen).

Kann mir einer bitte einen Tipp geben?

Hier ist mein Code. Vielen Dank!

public class WasBisherGutWar {
  double[] koeffizienten;

  public WasBisherGutWar(double...koeffizient) {
    this.koeffizienten = koeffizient;
    for (double i = koeffizient.length - 1; i >= 0; i--) {
      if (this.koeffizienten[(int) i] != 0) {

      }
    }
  }

  public double[] getKoeffizient() {
    return koeffizienten;
  }

  public void setKoeffizient(double[] koeffizient) {
    this.koeffizienten = koeffizient;
  }

  public String toString() {
    StringBuilder stringBuilder = new StringBuilder();

    for (double koeffizient: this.koeffizienten) {
      if (koeffizient != 0) {
        stringBuilder.append(koeffizient + ", ");
      }
    }

    return stringBuilder.toString();
  }

  public static void main(String[] args) {
    WasBisherGutWar p = new WasBisherGutWar(-3.0, -1.0, 0.0, 0.0, 1.0);
    System.out.println(p);
  }

}

...zum Beitrag

Raute rekursiv programmieren?

Hallo ich habe hier ein Problem bei der Programmierung. Hier ist meine Aufgabenstellung:

Schreiben Sie eine Anwendung Raute.java, welche ein Raute ausgibt. Der Nutzer soll zuvor die Größe n der Raute eingeben können. Bei geraden Eingaben (n gerade) soll der Text: „Das Programm arbeitet nur mit ungeraden Werten.“ ausgegeben werden. Bei ungeraden Eingaben (n ungerade) soll eine Raute der Höhe n ausgegeben werden.

Das ist mein Quellcode (allerdings kommt nicht ganz das raus was ich brauche^^):

/* 
 * Erzeugen einer Raute-rekursiv
 */
 
import java.util.Scanner; 

public class Raute {
  
  public static void main(String[] args) {
    Scanner scan = new Scanner(System.in);
 
    // Eingabe
    System.out.println("Geben Sie die Größe Ihrer Raute ein(nur ungerade Werte):");
    int groesse = scan.nextInt();

    // Bedingung --> gerade Werte werden nicht
    // vom Programm bearbeitet (+ Ausgabe)
    if (groesse % 2 == 0) {
       System.err.println("Das Programm arbeitet nur mit ungeraden Werten!");
    }
    else {
       // Berechnung:
       resultat(groesse);
    }
  }

  public static String methode1(int groesse) {

    if (groesse > 0) {
       return "* " + methode1(groesse - 1);
    }
    else {
       return " ";
    }
  }

  public static String methode2(int groesse) {

    if (groesse > 0) {
      return "* " + methode1(groesse - 1);
    }
    else {
      return " ";
    }
  }

  public static String space(int groesse) {

    if (groesse > 0) {
      return " " + space(groesse - 1);
    } 
    else {
      return " ";
    }
  }

  public static void resultat(int groesse) {
    
    for (int i = 1; i < groesse; i++) {
      System.out.println(space(groesse - i));
      System.out.println(methode1(i));
    }

    for (int i = 0; i < groesse; i++) {
      System.out.println(methode2(groesse - i));
      System.out.println(space(i));
    }
  }
}

Z.B.: groesse = 5

Ausgabe:

*   

  

* *   

  

* * *   

* * * *  

 

* * *  

 

* *

  

*

...zum Beitrag

Wie kann ich dieses switch-case in if umwandeln?

Hallo,

meine Aufgabe lautet, dass ich dieses switch-case in if-Verzweigungen umwandeln soll:

int choice = 2;

switch (choice) {
  case 1:
  case 2:
    System.out.print("Feuer");
    break;
  case 3:
    System.out.print("Luft");
    break;
  default:
    System.out.print("ungültig");
}

Und meine if-Verzweigung sieht so aus:

public class choice {
  public static void main(String[] args) {
    int choice = 2;

    if (choice >= 1) {
      System.out.println("Feuer");
      return;
    }

    if (choice == 2) {
      System.out.println("Feuer");
      return;
    }

    if (choice <= 3) {
      System.out.println("Luft");
      return;
    }
    else {
      System.out.println("ungueltig");
    }
  }
}

Aber beim Ausführen gibt er mir trotz Luft und else (ungültig) bei allen Zahlen Feuer aus. Weiß jemand warum?

...zum Beitrag

"Syntax error on token "else", delete this token" Fehlermeldung beseitigen?

Ich habe ein Bukkit Plugin programmieren Tutorial geguckt und bin auf folgendes Problem gestoßen, als ich das selbst ausprobiert hab:

package com.Akutaplug;

import org.bukkit.command.Command;

import org.bukkit.command.CommandSender;

import org.bukkit.entity.Player;

import org.bukkit.plugin.java.JavaPlugin;

public class Akutaplug extends JavaPlugin {

private static final String ChatColor = null;
private static final String Chatcolor = null;
public void onEnable() {
    // TODO Auto-generated method stub
    super.onEnable();
    
    System.out.println("TESTAUSGABE Akutaplug von Akutasan geladen.");
}

@Override
public boolean onCommand(CommandSender sender, Command command, String label, String[] args) {
    
    //Falls sender ein Player ist, machen wir den sender zum Player
    Player player = null;
    if(sender instanceof Player) {
        player = (Player) sender;
    }
    
    //Kommandos
        //Kommando "test"
        if(command.getName().equalsIgnoreCase("test"));
            
            if(player == null)
                sender.sendMessage("Glückwunsch! Der Test war erfolgreich!");
        return true;


} else {
    player.setHeatlth (20);
    player.
    player.sendMessage(ChatColor.GREEN + "[Akutaplugin] " + Chatcolor.WHITE +  " Glückwunsch! Der Test war erfolgreich!");
}

...zum Beitrag

[JAVA] Auf eine Methode in einer anderen Klasse zugreifen?

import static java.lang.System.out;
import java.util.Scanner;

public class Datentypen {
@SuppressWarnings("unused")
public static void main(String[] args){
    
    Scanner  keyboard = new Scanner(System.in);
    
    out.println("In Java gibt es viele verschiedene Datentypen. Da ich Ihnen die Unübersichtlichkeit sparen möchte,");
    out.println("habe ich dieses Programm geschrieben. Dieses Programm enthält jeweils ein Beispiel zu je einem Datentypen.");
    out.println("Also, worauf warten Sie? Suchen Sie sich einen Datentypen aus!");
    out.println();
    out.println("Boolean        Char");
    out.println("Byte       Short");
    out.println("Int        Long");
    out.println("Float      Double");
    
    String datentypen  = keyboard.next();
            
    switch(datentypen){
    case "Boolean":
        booleantyp();              //Fehler ist hier!
    }
    }


}

Zweite Klasse:

public class DatentypenMethoden {
public static void maint(String[] args){
    
}

public void booleantyp(){
    
}
}

Wie greife ich jetzt von der Klasse Datentypen auf die Methode "booleantyp()"?

...zum Beitrag

Taschenrechner programmiert (Java)?

Was würdet ihr verbessern rein von der Struktur.

import java.util.Scanner;
public class App {
    public static void main(String[] args) throws Exception {
        
        Scanner scanner = new Scanner(System.in);


        System.out.println("Bitte geben Sie erste Zahl ein: ");
        double zahl1 = scanner.nextDouble();


        System.out.println("Bitte geben Sie zweite Zahl ein: ");
        double zahl2 = scanner.nextDouble();


        System.out.println("Bitte geben Sie den Operator ein: ");
        char operator = scanner.next().charAt(0);


        System.out.println(taschenrechner(zahl1, zahl2, operator));


        
    }
    static double taschenrechner (double zahl1, double zahl2, char operator) {
            
        double ergebnis = 0.0;
        
        if (operator == '-') {
            ergebnis = zahl1 - zahl2;
        } else if (operator == '+') {
            ergebnis = zahl1 + zahl2;
        } else if (operator == '*') {
            ergebnis = zahl1 * zahl2;
        } else if (operator == '/') {
            ergebnis = zahl1 / zahl2;
        }
            return ergebnis;
    }
    
}

...zum Beitrag

Java return bedeutung?

Hallo, zb habe ich hier stehen:

public static final double R = 18;

public static double berechneDruck(double v,double t){ 
        return R *t/v;
}

was genau macht das return hier? kann mit das bitte einer ganz einfach erklären^^ danke:)

...zum Beitrag

Java: Methode wird nicht erkannt?

Hallo, ich arbeite gerade an einem Text Adventure. Intellij erkennt meine Methoden nicht. Hat jemand Lösungsvorschläge?

Code:

public class main {
    public static void main (String[] args){
        player();
        enemies();
        cases();
    }
    public static void player() {
        String name = "Shadow";
        int health = 50;
        int damage = 30;
    }
    public static void enemies() {
            public static void dragon() {
                String name = "Barbaton";
                int health = 100;
                int damage = 40;
            }
            public static void lion() {
                String name = "Eon";
                int health = 85;
                int damage = 55;
            }
            public static void pig() {
                String name = "Memba";
                int health = 20;
                int damage = 5;
            }
            public static void frog() {
                String name = "Zee";
                int health = 5;
                int damage = 1;
            }
            public static void zebra() {
                String name = "Zoy";
                int health = 28;
                int damage = 18;
            }
            public static void monkey() {
                String name = "Bart";
                int health = 45;
                int damage = 38;
            }
            public static void fox() {
                String name = "Foxie";
                int health = 35;
                int damage = 24;
            }
        }
    }
    public static void cases() {
        int min = 1;
        int max = 8;
        int random_int = (int)Math.floor(Math.random()*(max-min+1)+min);
        if(random_int == 1){
            System.out.println("Du hast Barbaton(Drache) als Gegner bekommen.");
        }
        else if (random_int == 2){
            System.out.println("Du hast Eon(Löwe) als Gegner bekommen.");
        }
        else if (random_int == 3){
            System.out.println("Du hast Memba(Schwein) als Gegner bekommen.");
        }
        else if (random_int == 4){
            System.out.println("Du hast Zee(Frosch) als Gegner bekommen.");
        }
        else if (random_int == 5){
            System.out.println("Du hast Zoy(Zebra) als Gegner bekommen.");
        }
        else if (random_int == 6){
            System.out.println("Du hast Bart(Affe) als Gegner bekommen.");
        }
        else if (random_int == 7){
            System.out.println("Du hast Foxie(Fuchs) als Gegner bekommen.");
        }
        else {
            System.out.println("");
        }
    }
}

...zum Beitrag

Ich muss diesen selbst programmierten Code (Bisektionsverfahren) rekursiv darstellen, jedoch tue ich mir da schwer. Kann mir jemand zur Hand gehen?

public class Bisektion {

public static void main(String[] args) {

    double Nst = bisektion(-10, 10, 0.01);
    System.out.println("Ermittelte Nullstelle: " + Nst);
    System.out.println("Funktionswert an dieser Stelle: " + fkt1(Nst));
    System.out.println();
    double Nst2 = bisektion(-1000, 1000, 0.01);
    System.out.println("Ermittelte Nullstelle: " + Nst2);
    System.out.println("Funktionswert an dieser Stelle: " + fkt2(Nst2));

}

// Test Funktionen
public static double fkt1(double x) {

    double fx;
    //fx = x * x * x - 24 * x * x + 59 * x + 420;
    fx = x + 5;
    return fx;
}

public static double fkt2(double x) {

    double fx2;
    fx2 = -1/Math.exp(x) + 1e20;

    return fx2;
}

public static double bisektion(double lower, double upper, double epsilon) {

    double mid = lower;
    double width = upper - lower; //20
    // Intervall
    while (width > epsilon) { //20 > 0.1

        mid = (lower + upper) / 2;//0   //-5
        if (fkt1(lower) * fkt1(mid) <= 0) { // if root is in [lower, mid]    //-5 * 0
            upper = mid;                    // move upper left               //upper = 0
        } else {                            // else root is in (mid, upper]
            lower = mid;                    // move lower right
        }
        width = upper - lower;                                               //width = 10
        System.out.println("root = " + mid );
    }
    return mid;
}

} // f(lower)<0 und f(upper)>0 // f besitzt nullstelle im Intervall [lower,upper] // middle // entweder lower oder upper durch ein kriterium mit middle ersetzen // stoppen wenn funktionswert näherungsweise 0 ist // ==> betrag kleiner als vorgegebene zahl epsilon

...zum Beitrag

Was möchtest Du wissen?

Deine Frage stellen