Wie berechne ich die folgende Expotentialgleichung?
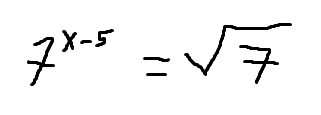
Ich möchte diese Aufgabe mit dem natürlichen Logarithmus also IN lösen.
Meine Idee wäre wie folgt.
4 Antworten
7ˣ¯⁵ = √7
ln(7ˣ¯⁵) = ln(√7)
(x−5)⋅ln(7) = ½⋅ln(7)
x−5 = ½
x = 5½
ln(aᵇ)=b⋅ln(a), und dann mußt Du nur noch die Wurzel als Exponent schreiben: √7=7^½
Du kannst über die Formel-Funktion hier auf GF auch Formeln über TeX Notation schreiben. Dann musst Du dich nicht mit irgendwelchen Symbolen abkaspern um die Gleichung abzubilden :-).
In Kommentaren geht das nicht, und außerdem finde ich den Formeleditor inflexibel und unangenehm. Wenn die Formeln happig sind, dann schreibe ich sie in echtem LaTeX und kopiere sie als Bild hinein, wenn sie simpel sind, dann mache ich es ganz flott über Unicode — das ist null Aufwand, weil ich alle Symbole auf der Tastatur habe (Compose-Taste mit vielen eigenen Definitionen).
Exponenten gleich setzen:
x - 5 = 1 / 2
x = 11 / 2
Verwende die Beziehung
Du erhältst:
Da die Basen gleich sind, führt das auf die Gleichung
Da die Potenzen links und rechts (sqrt(7)=7^0.5) die gleiche Basis haben, kannst du einfach x-5 mit 0.5 gleich setzen:
7^(x-5)=sqrt(7)
7^(x-5)=7^0.5
x-5=0.5
x=5.5
Alternativ:
7^(x-5)=sqrt(7)
7^(x-5)=7^0.5
ln(7^(x-5))=ln(7^0.5)
(x-5)*ln(7)=0.5*ln(7)
x-5=0.5
x=5.5
sqrt(n) ist die Quadratwurzel von n.
woher nimmst du die 1/2*?