Kann mir bitte jemand die Aufgabe lösen?
Hallo, kann mir jemand bitte die folgende Aufgabe lösen? In der Lösung gibt es nur das Endergebnis, aber nicht die Lösungswege.
MfG
3 Antworten
Aufgabe 18
Geg. Zylinder: h(Zyl) = 9,6 cm ; V(Zyl) = 850 cm³
Geg. Fünfeckpyramide: a(Pyr) = 8,0 cm ;
---
Zylinder r berechnen
V = r(Zyl)² * PI * h(Zyl)
r(Zyl) = Wurzel(V(Zyl) / PI / h(Zyl))
r(Zyl) = Wurzel(850 / PI() / 9,6)
r(Zyl) = 5,308831 cm
---
Mantelfläche Zylinder
M(Zyl) = r(Zyl) * 2 * PI * h(Zyl)
M(Zyl) = 5,308831 * 2 * PI() * 9,6
M(Zyl) = 320,2211418 cm²
---
Fünfeckpyramide hs berechnen
M = (a(Pyr)/2) * hs * n
hs = M / (a(Pyr)/2) / 5
hs = 320,2211418 / (8/2) / 5
hs = 320,2211418 / 4 / 5
hs = 16,01105709 cm
---
Fünfeckpyramide s berechnen
s = Wurzel(hs² + (a/2)²)
s = Wurzel(16,01105709^2 + (a/2)^2)
s = 16,5031496732969 cm
---
Fünfeckpyramide hs berechnen
r(Pyr) = (a/2) / sin(alpha)
r(Pyr) = (8/2) / sin(36)
r(Pyr) = 6,805206 cm
---
h = Wurzel(s(Pyr)² - r(Pyr)²)
h = Wurzel(16,50314967^2 - 6,805206^2)
h = 15,034730 cm
Die Höhe der Pyramide beträgt 15,03 cm
---
Mantelfläche Fünfeckpyramide
M = (a(Pyr)/2) * hs(Pyr) * n
M = (8/2) * 16,01105709 * 5
M = 320,2211418
ich hoffe ich liege auch richtig : Ich habe auf s verzichtet und stattdessen die Höhe des Bodendreiecks verwendet . . Danach dann Tangens
Berechne erst die Mantelfläche des Zylinders, und stelle dann die Formel für die Pyramide nach der Höhe der Seitenfläche um. Da muss dann noch a und die Mantelfläche des Zylinders eingesetzt werden, mit dem Tangens die Strecke h berechnet werden, und du hast die Lösung.
Die Höhe eines Dreiecks an der Mantelfläche berechnet.
ok , das ist gut . Aber das ist nicht die gesuchte Höhe der Py .
jo habe ich auch .
Nun hast du zwei komplette Antworten . Merkurus hat erst noch die Seitenkante berechnet und kann daher dann sinus nutzen
Ganz schön umfangreiche Aufgabe . Aber ohne Tangens, Sinus und Co läuft es nicht.
stelle dann die Formel für die Pyramide nach der Höhe um
In welcher Mantelformel kommt die Höhe der Pyramide vor ?
aber das h ist nicht die Höhe der Pyramide , sondern ha , die Höhe auf a !
Stimmt, mein Fehler. Danke für den Hinweis, ich habe meine Antwort revidiert.
Für M-Zy man braucht r aus
V-Zy = pi*r²*h
wurz(V/(pi*h) = r
w(850/(pi*9.6)) = 5.31 = r
.
M-Zy = 2pi*r*h
2pi*5.31*9.6 = 320.29
.
M-Py = 5*a*ha/2
also weil gleich zu M-Zy
320.29 = 5*8*ha/2
2*320.29/40 = ha = 16.01
.
ha ist die Höhe der Seitenflächen
Die braucht man als Zwischenergebnis
.
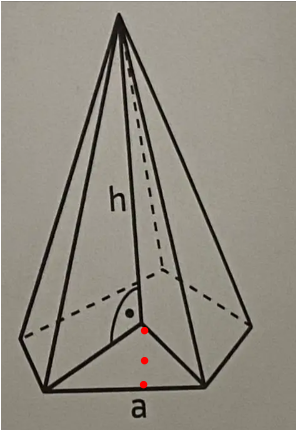
diese Strecke s noch : tan(36) = (8/2)/s
s = 4/tan(36°) = 5.51
und nun ............ (ha)² = (h-py)² + s²
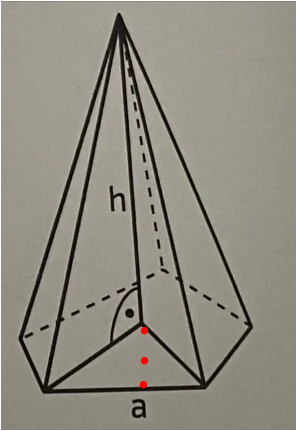
Sind alle Seiten der 5 Dreiecke an der Grundfläche nicht gleich groß? Kann man da kein Pythagoras verwenden, wo es auf dem Bild markiert ist?
Ich bekomme 14,43cm raus. In der Lösung steht 15cm.