Ebenengleichung aufstellen?

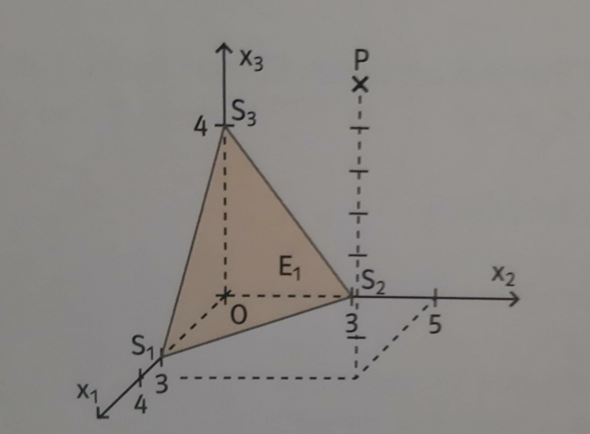
In nebenstehender Figur ist ein Ausschnitt der Ebene E, und der Punkt P dargestellt. Bestimmen Sie den Abstand des Punktes P von der Ebene E₁.

Wie bestimme ich überhaupt die Ebenengleichung in Koordinatenform?

Answer 1

[mihisu]

Im konkreten Fall geht das mit den gegebenen Schnittpunkten mit den Koordinatenachsen relativ schnell und einfach, da bei diesen Punkt nur eine Koordinate ungleich 0 ist.

Ansatz für die Ebenengleichung:

$n_1\cdot x_1+n_2\cdot x_2+n_3\cdot x_3=c$

Einsetzen von S₁(3 | 0 | 0):

$n_1\cdot 3=c\quad \rightarrow\quad n_1=\frac{1}{3}\cdot c$

Einsetzen von S₂(0 | 3 | 0):

$n_2\cdot 3=c\quad \rightarrow\quad n_2=\frac{1}{3}\cdot c$

Einsetzen von S₃(0 | 0 | 4):

$n_3\cdot 4=c\quad \rightarrow\quad n_3=\frac{1}{4}\cdot c$

Damit erhält man für die Ebenengleichung:

$\frac{1}{3}\cdot c\cdot x_1+\frac{1}{3}\cdot c\cdot x_2+\frac{1}{4}\cdot c\cdot x_3=c$

Für jede Wahl von c (mit Ausnahme von c = 0) ist nun eine Gleichung der Ebene E in Koordinatenform gegeben.

Man kann beispielsweise einfach c = 1 wählen und erhält:

$E:\ \frac{1}{3}\cdot x_1+\frac{1}{3}\cdot x_2+\frac{1}{4}\cdot x_3=1$

Oder, wenn man keine Brüche als Koeffizienten möchte, könnte man beispielsweise auch c = 12 wählen und erhält:

$E:\ 4\cdot x_1+4\cdot x_2+3\cdot x_3=12$

============

Alternativ kannst du auch den üblichen Weg gehen, dass du anhand der Punkte S₁(3 | 0 | 0) und S₂(0 | 3 | 0) und S₃(0 | 0 | 4) zwei Richtungsvektoren berechnest, und eine Ebenengleichung in Parameterform erhältst. Dann kannst du einen Normalenvektor über das Kreuzprodukt der beiden Richtungsvektoren erhalten, und damit dann eine Ebenengleichung in Normalenform bzw. dann ausmultipliziert in Koordinatenform erhalten.

============Ergänzung============

Für den Abstand vom Punkt P zur Ebene, brauchst du übrigens gar nicht unbedingt die Ebenengleichung. Ich würde dazu folgendermaßen vorgehen...

Betrachte die Vektoren:

$\vec{u}:=\overrightarrow{S_1S_2},\quad \vec{v}:=\overrightarrow{S_1S_3},\quad \vec{w}:=\overrightarrow{S_1P}$

Berechne mit Hilfe des Spatprodukts das Volumen eines entsprechenden Spats.

https://de.wikipedia.org/wiki/Spatprodukt

$V=\left(\vec{u}\times\vec{v}\right)\cdot \vec{w}$

Berechne den Flächeninhalt des durch die Vektoren u und v aufgespannten Parallelogramms mit Hilfe des Kreuzprodukts.

https://de.wikipedia.org/wiki/Kreuzprodukt

$A=\left\lvert\vec{u}\times\vec{v}\right\rvert$

Dann erhält man die entsprechende Höhe des Spats, die gleich dem gesuchten Abstand d des Punktes P von der Ebene E ist, indem man das Volumen durch den Flächeninhalt teilt...

$d=\frac{V}{A}=\frac{\left(\vec{u}\times\vec{v}\right)\cdot \vec{w}}{\left\lvert\vec{u}\times\vec{v}\right\rvert}$

Lösungsvorschlag mit dem zuletzt genannten Lösungsweg:

Comments

[kolapi]

und wie berechne ich bei der Alternative die zwei Richtungsvektoren? Die Methode hat mir am besten gefallen

[mihisu]

@kolapi

Naja, einfach mit „Spitze minus Fuß“...

Für den Vektor von S₁(3 | 0 | 0) zu S₂(0 | 3 | 0) erhält man dann [-3, 3, 0].
Für den Vektor von S₁(3 | 0 | 0) zu S₃(0 | 0 | 4) erhält man dann [-3, 0, 4].

Das Kreuzprodukt der beiden Vektoren ist dann [12, 12, 9]. Dementsprechend kann man dann [12, 12, 9] als einen Normalenvektor der Ebene E verwenden.

Dementsprechend kann man dann eine Ebenengleichung in Normalform aufstellen (indem man beispielsweise außerdem noch S₁(3 | 0 | 0) noch als Stützpunkt verwendet)...

[12, 12, 9] ⋅ (x - [3, 0, 0]) = 0

Ausmultiplizieren liefert dann...

[12, 12, 9] ⋅ x - [12, 12, 9] ⋅ [3, 0, 0] = 0

[12, 12, 9] ⋅ x - (12 ⋅ 3 + 12 ⋅ 0 + 9 ⋅ 0) = 0

[12, 12, 9] ⋅ x - 36 = 0

[12, 12, 9] ⋅ x = 36

Bzw. wenn man auch den Vektor x = [x₁, x₂, x₃] ausschreibt und ausmultipliziert...

12x₁ + 12x₂ + 9x₃ = 36

Answer 2

[Vi2ZE]

Ich habe jetzt die Punkte P(0|0|0), Q(3|0|0) und R(0|0|4) in der Ebene E abgelesen.

Um die Koordinatenform von E zu bestimmen, musst du folgende Schritte machen:

PQ = (3|0|0) und PR = (0|0|4)

N = PQ x PR = (0|-12|0)

a * x1 + b * x2 + c * x3 = d 0 * x1 - 12 * x2 + 0 * x3 = d

P(0|0|0) einsetzen: 0 * 0 - 12 * 0 + 0 * 0 = d d = 0

-12 * x2 = 0

Um den Abstand des Punktes P(4|5|7) von der Ebene E zu berechnen, musst du folgende Schritte machen:

Setze die Werte von a, b, c, d, x1, x2 und x3 in die Formel ein: d = |-12 * 5 - 0| / √(-12^2 + 0^2 + 0^2)

Vereinfache den Ausdruck: d = | -60 | / √144 d = 60 / 12

Schreibe das Ergebnis auf: d = 5

Der Abstand des Punktes P(4|5|7) von der Ebene E beträgt 5 Längeneinheiten.

Comments

[kolapi]

Warum P(0,0,0) ? S1 ist doch z.B. in der Ebene mit S2(0,3,0)

[MichaelH77]

@kolapi

der Ursprung gehört nicht zur Ebene, stattdessen muss z.B. (0|3|0) verwendet werden