Quadratische betragsungleichung?
Kann mir jmd sagen wie man diese Ungleichung mittels fallunterscheidung lösen kann? .
Danke im voraus
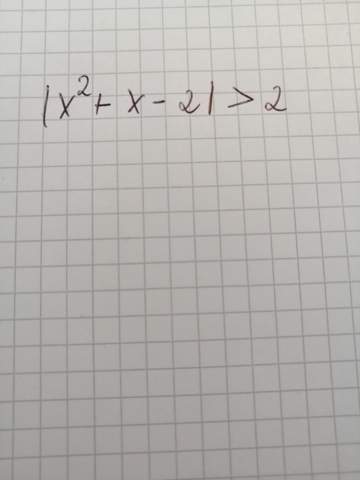
2 Antworten
Also, es ist gegeben:
Du musst quasi die markanten x-Stellen finden, wo "x² + x - 2 = 0" gilt. Genrell musst du dann Bereiche auswählen wo du dann ohne Betrag schreiben kannst.
Die Nullstellen von "x² + x - 2 = 0" findest du hier mit der pq-Formel, also:
also x_1 = 1 oder x_2 = -2 .
Wenn du Werte einsetzt, oder den Graphen gezeichnet hast, wirst du feststellen, dass
der Term "x² + x - 2 = 0" Positiv ist und für
also für diese x-Werte der Term "x² +x -2" negativ.
Also hast du zu lösen zwei Ungleichungen, nach dem eben gesagten mit:
I. x² + x - 2 >= 2 für alle x wie in (b) oben (hier ist ja derBetrag erfüllt) sowie
II. -x² - x + 2 > 2 nach oben (a), weil hier der Betrag verletzt werden würde... Daher muss ich das umschreiben.
Betrag von 0 ist ja erlaubt.
Viel Spaß!
Anmerkung: I. und II. sind sehr leicht zu lösen, wenn man alle x-Variablen auf einer Seite hat und dann jeweils ein x ausklammert.
Bei Multiplikation mit einer negatvien Zahl dreht sich die das Zeichen "<" um (bzw. das Zeichen ">")!
Ja, die anderen gleichungen kann der machen... soll arbeiten für sein Abitur
Ah ok 😁. Statt danke, aber.. Kam auch nur ein abruptes "und was ist".
(X^2+x-2)^2>4
X^4+x^3-2x^2+x^3+x^2-2x-2x^2-2x>0
X^4+2x^3-3x^2-4x>0
X(x^3+2x^2-3x-4)>0
X1=0
X2=-1
X(x+1)(x^2+x-4) >0
X3=-1/2+wurzel (1/4+4) =-1/2+wurzel(17/4)=1,561
X4=-1/2-wurzel (17/4)=-2,561
-unendlich<x<-2,561
-1<x<0
1,561<x<+unendlich
Eigentlich wüsste ich nicht wo. Hab die Zahlen auch zur Probe eingesetzt und passt.
Sorry aber hab nach dem rechenweg gefragt und deine Lösung ist falsch
Die darfst du machen...