Gebrochen Rationale Ungleichung mit Betrag im Nenner?
Hallo zusammen,
ich habe folende Gleichung gegeben:
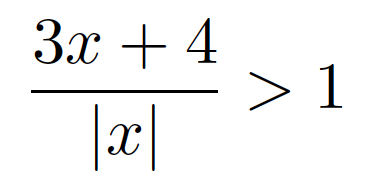
Im ersten Fall betrachte Ich x > 0:
Hier ist für mich noch alles klar.
Was passiert aber im zweiten Fall wenn x < 0 ist?
Muss ich dann alle x, so wohl im Nenner als auch im Zähler negativ setzen?
Lautet dann meine Gleichung so:
3x+4 < -x (Nur das betrachtete x negativ)
oder
3*(-x)+4 < -x (Oder alle x Negativ)
Ich steh hier gerade auf dem Schlauch. Vielleicht kann mir ja einer kurz weiter helfen und erklären ob ich alle x anpassen muss oder nur das x welches in der Fallunterscheidung betrachtet wird.
Viele Grüße
2 Antworten
Hallo,
im Fall x>=0 läßt Du die Betragsstriche einfach weg und bekommst als Lösungsmenge x>=0 heraus. Daß auch x zwischen -2 und 0 die Gleichung löst, ist hier ohne Belang, weil diese erste Gleichung nur für nichtnegative x definiert ist.
Im zweiten Fall ersetzt Du das |x| im Nenner durch -x.
(3x+4)/(-x)>1.
Beide Seiten mit (-x) multiplizieren ergibt 3x+4>-x.
Das Ungleichheitszeichen darfst Du in diesem Fall nicht umdrehen, denn da x hier nur eine negative Zahl sein kann, ist -x positiv.
Das ergibt 4x>-4, also x>-1.
Zusammen mit der Lösungsmenge des ersten Falls für x>=0 bekommst Du die Lösungsmenge {x|x>-1}
Herzliche Grüße,
Willy
Du darfst es gar nicht umdrehen, denn |x| ist auf jeden Fall größer oder gleich Null, egal, welchen Wert x selbst haben kann.
Multipliziere zuerst mit |x| und mach dann erst die Fallunterscheidung, dann siehst Du es.
Die Lösungsmenge für beide Fälle ist x>-1. Wenn Du mir nicht glaubst, gib die Gleichung in einen Plotter ein, dann siehst Du es selbst.
Da du den Fall betrachtest, für den x kleiner 0 ist, ist -x (womit du multiplizierst) ja positiv.
Man sollte bei der Lösungsmenge noch die Definitionsmenge berücksichtigen, also dass x ungleich Null ist: L = (-1 ; 0) ∪ (0 ; ∞)
Das obere x darfst du nicht anfassen, da das nicht in Betragsstrichen steht. Rumspielen darfst du nur mit dem unteren x in Betragsstrichen.
Für x < 0 gilt:
(3x + 4) / ∣x∣ < 1 ∣*(-1)
(3x + 4) / ((-1) * x) > 1
- (3x + 4) / x > 1
Bist du dir sicher, dass man das > hier nicht umdrehen muss? Im Zweiten Fall darf ich ja nur negative Zahlen einsetzen. Sobald ich etwas mit einer negativen Zahl multipliziere oder dividiere, dreht sich das Zeichen immer um. Wieso soll das hier nicht der Fall sein?