Wie muss man die Gleichung wählen (a E R), dass die Gleichung x2=3+(ax-3)2 nur eine Lösung hat?
(habe mehrere Stunden heute verschwendet wäre dir dankbar!)
Die beigefügte Notiz zeigt a=2 v a=-2, auf das bin ich gekommen, aber ich weiß nicht wie ich auf den restlichen Teil der Lösung komme.
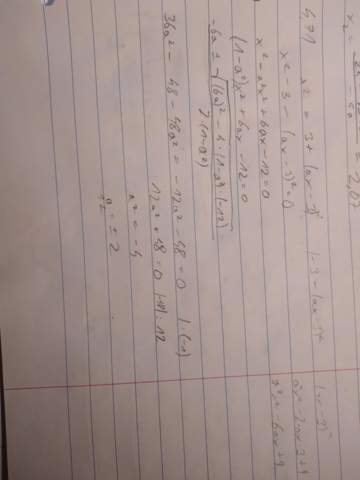
Die finale Antwort lautet
(brauche aber Rechenweg):
x2=3+(ax-3)2
(a2-1)×x2-6ax+12=0
Die Gleichung hat genau eine Lösung, wenn a=1 v a=-1 v a=2 v a=-2
Lösung lautet für a=1 x=2
für a=-1 x=2
für a= 2 x=2
für a=-2 x=-2
4 Antworten
die quadratische Gleichung hat nur eine Lösung, wenn der Ausdruck unter der Wurzel 0 ist
beim nullsetzen des Ausdrucks unter der Wurzel ist dir ein Vorzeichenfehler passiert
es muss heißen: 36a²+48-48a²=0
daraus dann 12a²=48
oder a²=4
a=2 oder a=-2
(abc-Formel ohne Wurzel, da diese 0 ist)
für a=2 erhält man x=-12/(2*(-3)) = 2
für a=-2: x=12/(2(-3)) = -2
für diese beiden a hat die Ausgangsgleichung nur eine Lösung
auf a=1 und a=-1 kommt man, wenn man die Klammer vor dem x² null setzt, also wenn das x² wegfällt
dann hat man keine quadratische Gleichung mehr, sondern nur noch
für a=1:
x²=3+(x-3)² bzw 0=-6x+12 also x=2
für a=-1:
x²=3+(x+3)² bzw 0=6x+12 also x=-2
x=2 für a=1
x=-2 für a=-1
bei Anwendung der Lösungsformel erhält man den Nenner 2(1-a²) Dieser darf nicht null werden. Das wäre für a=1 oder a=-1 der Fall. Diese beiden Fälle untersucht man dann in der Ausgangsgleichung also x²=3+(ax-3)², in dem man die Werte für a einsetzt:
für a=1 erhält man x²=3+(x-3)². Dann rechnet man rechts die binomische Formel aus. Dann kann man auf beiden Seiten x² subtrahieren, man erhält die einfache Gleichung 6x=12 also x=2
entsprechend für a=-1. Dort habe ich vor Anwendung der binomischen Formel das Minus ausgeklammert:
x²=3+(-x-3)²
x²=3+[-(x+3)]²
beim quadrieren fällt das Minus weg:
x²=3+(x+3)²
binomische Formel:
x²=3+x²+6x+9
x² auf beiden Seiten subtrahieren und zusammenfassen:
-12=6x
x=-2
Eine quadratische Gleichung hat genau dann genau eine reelle Lösung, wenn die Diskriminante (Wert unter der Wurzel in der Mitternachtsformel) den Wert 0 hat. Also einfach D = 0. Mit D = b² - 4a c.
Gleichung a x² + b x + c = 0
Die von dir angegebene finale Antwort kann auch nicht ganz stimmen:
(a2-1)×x2-6ax+12=0...hier gehört -12
Die Lösung a= +1 scheint mir auch nicht möglich, da (a²-1) dann 0 wäre.
Bei der Lösung a=-1 würde obige Gleichung aufgehen, aber in deiner Zettel-Lösung würde a=-1 zum Nenner 0 führen (!).
auf den Nenner kommt man bei a=1 oder a=-1 erst gar nicht, weil die Gleichung dann kein x² mehr enthält. Man muss a=1 oder a=-1 in die Ausgangsgleichung einsetzen
Du hast einen Vorzeichenfehler in der 4.letzten Zeile, es muss +48 heißen.
Zum Glück, denn für a²=-4 gibt es in R keine Lösung!
Hallo, danke erstmal. Mir ist nur noch nicht ganz klar wie das "x²=3+(x-3)² bzw 0=-6x+12" zu stande kommt, denn da muss ich ja wissen, dass ich a=1 einsetze. Wie komme ich darauf ausgerechnet a=+-1 einzusetzen?