Mathe Aufgabe - Lösungsansatz?
aufgabe: Die Parabel zur Funktionsgleichung
f (x) = -x^2 + 9 ist gegeben.
Ein Dreieck wird in den Bereich zwischen Parabel und x-Achse so gelegt, dass ein Eckpunkt beim Koordinatenursprung liegt und die beiden anderen Punkte auf der Parabel auf gleicher Höhe liegen, sodass die entsprechende Dreiecksseite parallel zur x-Achse liegt. Berechnen Sie die Koordinaten des Punktes P, sodass das Dreieck den maximalen Flächeninhalt besitzt.
gehe wie folgt vor beim Lösen:
Extremale Größe
Haupt- und nebenbedingung
Zielfunktion
—————-
ich weiß dass die hauptbedibgung 1/2*gh ist
und die nebenbedingung ist die Funktionsgleichung
aber weiter komm ich nicht kann mir bitte jemand helfen
3 Antworten
Ableitung machen und Nullpunkte bestimmen, wäre ein Ansatz.
Ein Dreieck hat die Fläche 1/2 * Grundlinie * Höhe. Die Grundlinie ist 2x
Nebenbedingung
Damit:
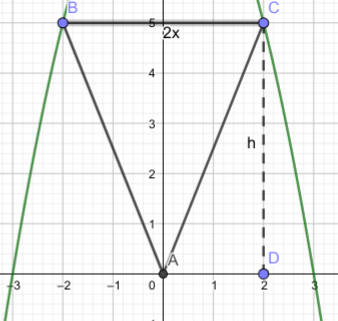
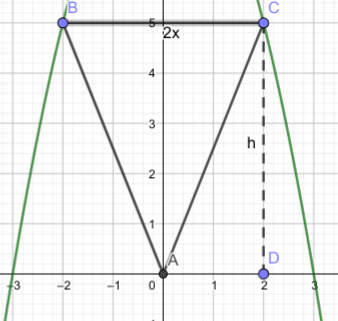
Skizze:
Links und rechts von der y-Achse x-(-x) = 2x in der Skizze 2-(-2) = 4
Danke dir so sehr aber könntest du das bitte etwas ausführlicher erklären also wie du zu allem gekommen bist
Steht jeder Schritt da. Wenn man allerdings nicht weiß, wie man die Fläche eines Dreiecks berechnet, kann man die Aufgabe nicht lösen und der Lösung auch nicht folgen. Ich wüsste nun keinen einzigen Satz, um das ausführlicher zu erklären und in der Skizze habe ich auch die Höhe "h" noch absichtlich so eingezeichnet, dass man erkennt, was das mit f(x) (=y) zu tun hat.
Und jetzt geht die Aufgabe eigentlich erst richtig los, denn man muss ja noch das Maximum suchen.
Hab es verstanden aber wie kommst du zu der Zielfunktion
Die Nebenbedingung einfach eingesetzt in die Funktion zur Berechnung der Fläche. Beachte , dass aus A(x,y) eine Funktion A(x) nur "von x" wird, indem "y" in A(x;y) durch den Funktionsterm "-x²+9" ersetzt wird ("y" ist die Höhe des Dreiecks)
Und natürlich 2 mit 1/2 zu 1 verrechnet.
was ist fie hauptbedibgung wenn es heißt die Summe aus den beiden Produkten soll 100 ergeben
Was soll das jetzt mit dieser Aufgabe zu tun haben? Außerdem klingt das eher wie eine Nebenbedingung - Poste bitte eine neue Frage, wenn es eine neue Aufgabe ist.
Bei der Hauptbedingung kannst du h durch f(x) ersetzen, da das auch die Höhe beschreibt. g kannst du ersetzen durch 2x da der Graph Achsen symmetrisch ist, ist die x Koordinate die Länge der einen Hälfte. Um die Länge der gesamten Grundfläche raus zu kriegen, musst du X mal zwei nehmen. Jetzt leitest du die erhaltene Funktion für den Flächeninhalt ab und suchst nach Hoch– beziehungsweise Tiefpunkten
Wieso ist die Grundlinie 2x