Extremalaufgaben! Mathe! Hilfe!
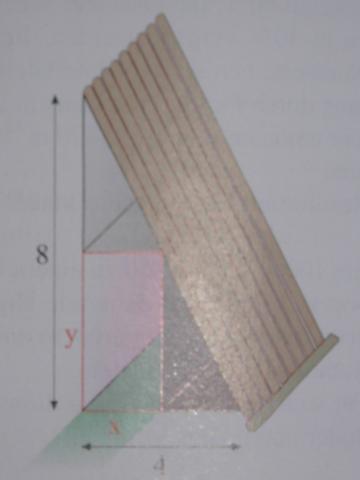
Kann mir jemand sagen, wie ich auf die Nebenbedingungen komme, bzw. weiter zur Zielfunktion? Die Aufgabe ist, die Fläche xy maximal werden zu lassen (siehe Skizze), also hab ich die Hauptbedingung A=xy aufgestellt. Des weiteren hab ich die Seite des Dreiecks mit den Baumstämmen ausgerechnet. Sie beträgt 12. Welche Nebenbedingungen gelten noch ode wie komm ich weiter? BITTE HELFT MIR!
5 Antworten
Ich nehme an, dass die du größtmögliche Fläche finden sollst (was du nicht angibst).
Dann würde ich wie JJcool vorgehen. Die Geradengleichung lässt sich durch Einsetzen der Koordinaten der Punkte ( 0 | 8 ) und ( 4 | 0 ) in die allgemeine Form der Geradengleichung leicht bestimmen.
Ergebnis: Die größtmöglichen Fläche von A = 8 LE² entsteht von x = 2 LE.
Gerade bei Rechtecken hat man immer nahezu dieselbe Vorgehensweise. Man bekommt die Länge eines Umfangs oder die Fläche als Zahl gegeben, und aus der Flächenformel erhält man die Zielfunktion.
Denn du kannst das Rechteck meist so hinlegen, dass du setzen kannst:
u = 2x + 2y
A = x y
Da y = f(x) eine Funktion von x ist, rechnest du aus der Umfangsformel eine Seite aus und setzt sie in die Flächenformel ein.(Oder umgekehrt.) Ausgeklammert führt das zu einer Gleichung 3. Grades, die du ableiten kannst.
- Ableitung gleich Null ergibt Extremwerte, und das ist dann ja eine gesuchte Maximierung oder Minimierung der Fläche.
Das ist ein Prototyp. Aber irgendwie zwei solcher Beziehungen findest du immer. Das sind dann Nebenbedingung und Zielfunktion.
Versuch doch mal die Bretter als Gerade darzustellen und du nimmst die Ecke links Unten als Koordinatenursprung. Wenn du eine geeignete Gerade gefunden hast, kannst du die Fläche ja über x * f(x) berechnen. Versuch das einfach mal mit dem Ansatz oder frag nochmal nach wenn du nicht weiter kommst :)
Nebenbedingung ergibt sich durch den Strahlensatz;
y/4 = (4-x)/4 und nach y auflösen und in Hauptbed. einsetzen usw
Des weiteren hab ich die Seite des Dreiecks mit den Baumstämmen ausgerechnet. Sie beträgt 12.
Interessant.