

siehe:
https://www.youtube.com/watch?v=GJIhJAtnLn8


siehe:
https://www.youtube.com/watch?v=GJIhJAtnLn8


c_1 = c_2 = c / 2 (Seitenhalbierende)
s_c mittels Kosinussatz in Dreieck ADC (α, c_1 und b bekannt)
γ_1 und γ_2 mittels Sinussatz
Ergänzung:
Aus der Aufgabenstellung geht nicht eindeutig hervor, ob bei a) γ_1, γ_2 und s_c gesucht sind. Man kann die Aufgabe auch so interpretieren, dass w_α sich auf a) und s_c sich auf b) bezieht und nur die fehlenden Größen von Dreieck ABC gesucht sind.
Beispiel b) ohne Kosinussatz:
s_c / sin(α) = b / sin(δ_1) mit δ_1 = Winkel CDA
δ_1 = 45,504°
δ_2 = 180° - δ_1 = 134,496° mit δ_2 = Winkel BDC
c_1 / sin(γ_1) = s_c / sin(α)
c_1 = 3,313
Berechnung von β:
(1) β + γ_2 = δ_1 ⇔ γ_2 = δ_1 - β
(2) sin(β) / s_c = sin(γ_2) / c_2
(1) in (2)
sin(β) / s_c = sin(δ_1 - β) / c_2
Additionstheorem für den Sinus:
(c_2 / s_c) * sin(β) = sin(δ_1) * cos(β) - cos(δ_1) * sin(β)
sin(β) ausklammern:
((c_2 / s_c) + cos(δ_1)) * sin(β) = sin(δ_1) * cos(β)
sin / cos = tan:
tan(β) = sin(δ_1) / ((c_2 / s_c) + cos(δ_1))
tan(β) = sin(45,504°) / ((3,313 / 6,5) + cos(45,504°)
β = 30,51°
Damit sind die Winkel und 2 Seiten von Dreieck DBC bekannt und a kann mit dem Sinussatz bestimmt werden. Ich bezweifel aber, dass diese Lösung einfacher ist, als die Anwendung des Kosinussatzes.


Unter der Voraussetzung, dass der obere Punkt auf der gegenüberliegenden Gewässerseite, der mittlere Punkt und der rechtwinklig 18 m vom Ufer abgesetzte Punkt auf einer Geraden liegen (diese Angabe fehlt), kann der Strahlensatz genutzt werden:
x / 15 = 18 / 30


blaue Fläche (sichtbar nach dem Umklappen):
A = (1 / 2) * 10 * x
x = 10 * tan(α)
α = 90° - 2 * β
tan(β) = 10 / 20
Die Fläche setzt Du ins Verhältnis zur Gesamtfläche.


Es hilft am meisten, wenn man die Aufgaben versteht und eigenständig löst. Am Schluss kann man dann die Lösungen vergleichen.


quadrieren, Bruch beseitigen, Klammern auflösen und zusammenfassen


Beginne mit der linken Parabel und nehme als Basis die Scheitelpunktform. Nutze die Koordinaten von S, um die Scheitelpunktform aufzustellen und setze die Koordinaten von Q ein, um den Steigungsfaktor a zu bestimmen.
Setze den x-Wert von P ein, um den zugehörigen y-Wert von P zu bestimmen.
Die Ableitung liefert die Steigung in P. Das ist auch die Steigung in P für die rechte Parabel.
Gehe für die rechte Parabel von der Normalform aus und leite diese ab. Mit P, N und der Steigung in P kannst Du drei Gleichungen aufstellen, um die unbekannten Parameter a, b und c der zweiten Parabel zu bestimmen.
Damit liegen die notwendigen Werte für die Integralrechnung (Volumenberechnung) vor.
...


Bilde 3 Gleichungen mit den Unbekannten λ, μ und k. Nutze die Gleichungen (2) und (3), um λ und μ zu bestimmen. Setze die berechneten Werte in Gleichung (1) ein und bestimme k. Zum Vergleich: k = 17


Die Funktion liegt in der Scheitelpunktform vor. Den Scheitelpunkt kannst Du direkt ablesen: S (40│10) Damit hast Du das Maximum.
Nullstellen:
0 = (-1/200) * (w - 40)² + 10
Der positive Wert ist gesucht.
Schnittpunkt mit der h-Achse:
h(0) = (-1/200) * (0 - 40)² + 10
An welchen Stellen hat der Speer 8 m Höhe?
8 = (-1/200) * (w - 40)² + 10
Hier kommen 2 Lösungen für w heraus.
Welche Höhe hat der Speer nach 70 m?
h(70) = (-1/200) * (70 - 40)² + 10


2 * x = x + x
2 * ln(5) = ln(5) + ln(5)
a^x * a^x = a^(x + x) = a^(2 * x)
e^ln(5) * e^ln(5) = e^(ln(5) + ln(5)) = e^(2 * ln(5))
Da e^ln(5) = 5 muss das das Produkt 25 sein.


Die Variablen werden mit Indizes unterschieden. Du kannst auch x₁ = x und x₂ = y setzen, wenn das besser verständlich ist.
zu a)
Setze a = 6 ein und löse das Gleichungssystem. Du erhältst x₁ und x₂ abhängig von b.
zu b)
Für a = -6 wird die linke Seite der zweiten Gleichung gleich Null. Wenn die rechte Seite ungleich Null ist, gibt es einen Widerspruch und damit keine Lösung. Bestimme also b so, dass die rechte Seite der Gleichung Null ergibt, also 4 + 2b = 0. Dann fällt die zweite Gleichung weg und es gibt unendlich viele Lösungen. x₁ kann dann abhängig von x₂ bestimmt werden.


Beispiel 1a)
1 / 2 = x / 10
Die Dreiecke sind ähnlich, sodass Du entsprechende Seiten ins Verhältnis zueinander setzen kannst.
...


f(x) = x² – x , x₀ = 1
Differenzenquotient:
(f(x₀ + h) – f(x₀)) / h =
((x₀ + h)² – (x₀ + h) - (x₀² - x₀)) / h =
(x₀² + 2 * x₀ * h + h² – x₀ – h - x₀² + x₀) / h =
(2 * x₀ * h + h² - h) / h =
2 * x₀ + h - 1
Differentialquotient:
lim(h → 0) (2 * x₀ + h – 1) = 2 * x₀ - 1
für x₀ = 1
lim(h → 0) (2 * 1 – 1) = 1


Taylorpolynom:
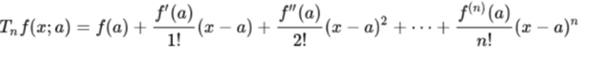
Beginne mit f(x₀), hier: f(1) = 5:
= 5 + 9 * (x - 1) / 1! + 16 * (x - 1)² / 2! + ...
...


Funktionsgleichung:
f(x) = a * x * (x - 7) * (x - 11)
P (3│4,3) einsetzen:
4,3 = a * 3 * (3 - 7) * (3 - 11)
a = 43 / 960
f(x) = (43 / 960) * x * (x - 7) * (x - 11)
a)
Gesucht ist die Fläche unter der Kurve.
∫ (43 / 960) * x * (x - 7) * (x - 11) dx von 0 bis 10 = 15,677...
11000 Liter + 15,677 * 1000 Liter = 26677 Liter
b)
t = 0 Minimal (zu Beginn, da Zulauf)
t = 7 Maximal (ab da Ablauf)
c)
Setze das Integral gleich 15 und bestimme die obere Schranke.
Die liegt bei ca. t = 4,5.
d)
Das gilt im Bereich des Abflusses, also z.B. bei t = 8.


1) AB mittels Kosinussatz
2) α (Dreieckswinkel in A) mittels Sinussatz
3) Höhe h = t mittels Sinus
4) Höhenfußpunktabschnitt (Abschnitt von A zum Höhenfußpunkt) mittels Kosinus
5) AP mittels Differenz zu 40


Du hast nicht alle Bedingungen ausgewertet.
Funktion und Ableitungen:
f(x) = ax³ + bx² + cx + d
f'(x) = 3ax² + 2bx + c
f''(x) = 6ax + 2b
Es gibt 4 Bedingungen und 4 Unbekannte.
Bedingungen:
(1) f(0) = 3
(2) f'(0) = 0
(3) f(1) = 5
(4) f''(1) = 0
Gleichungssystem:
(1) d = 3
(2) c = 0
(3) 5 = a + b + 3
(4) 0 = 6a + 2b
--------------------
Es reduziert sich auf ein LGS mit 2 Unbekannten.
Das führt zu a = -1 und b = 3. c und d sind ja schon bekannt.


Beachte die ähnlichen rechtwinkligen Dreiecke, die durch die Höhen h_a, h_b und h_c entstehen.
Voraussetzung: c_2 geht über A hinaus.
Strahlensatz:
h_b / h_c = a_1 / a_2
h_c / h_a = b_1 / b_2
h_a / h_b = c_1 / c_2
-------------------
(h_b / h_c) * (h_c / h_a) * (h_a / h_b) = (a_1 / a_2) * (b_1 / b_2) * (c_1 / c_2) = 1


2t -t³ = t - t²
t³ - t² -t = 0
t * (t² - t - 1) = 0
t_1 = 0
t² - t - 1 = 0
t = (1 / 2) +-√((1 / 2)² + 1)
t_2 = (1 / 2) * (1 + √5)
t_3 = (1 / 2) * (1 - √5)
Werte für t einsetzen und zugehörige x- und y- Werte ermitteln.


Bilde die Differenz der beiden Funktionen, also f(x) - g(x) und bestimme davon das Maximum.
Das funktioniert mittels Differentialrechnung (Ableitung gleich Null setzen) oder einfach, indem der Scheitelpunkt der Differenzfunktion bestimmt wird.
Zum Vergleich: Der größte Abstand liegt bei x = 35